Поиск Объекта по Кадастровому Или Условному Номеру
Консультации: государственный реестр 🌐 гражданский 🌐 единый государственный 🌐 единый государственный реестр 🌐 кадастровый номер 🌐 кодекс 🌐 объекте недвижимости 🌐 ознакомление 🌐 порядок 🌐 раздел 🌐 сроки 🌐 условный
Введите адрес или кадастровый номер участка🔻🔻🔻
Он должен указываться с двоеточиями, и содержать 4 группы цифр. Например, 77:08:0009005:8 Росреестр Найти Объект по Адресу
Публичная кадастровая карта России на
Поиск в Росреестре по Адресу По клику на участок официальной карты вы узнаете кадастровый номер объекта, площадь, назначение, год постройки (для дома) и можете перейти к просмотру всех доступных электронных выписок из ЕГРН.
- межевание не делалось вообще
- межевание сделано давно (до 2006 года)
- межевание сделано недавно (1-2 месяца назад)
- технические ошибки кадастровой карты
Сервис дает возможность приобретения пакетного предложения и получения выгодной скидки до 85%.
Росреестр Найти Объект по Адресу
Отчет об объекте недвижимости
Поиск в Росреестре по Адресу Для получения документа, необходимо найти требуемый объект в строке поиска по адресу или кадастровому номеру, ознакомиться с краткой информацией и перейти к оформлению заказа. Для просмотра образца отчета об объекте недвижимости необходимо перейти по ссылке.
- О характеристиках объекта и правах собственников. Документ включает в себя данные о настоящем владельце, кадастровую стоимость и информацию об обременениях.
- О переходе прав. Документ включает в себя историю всех владений.
- Расширенная выписка. Включает в себя полный пакет данных об объекте.
Росреестр Найти Объект по Адресу
Узнать кадастровый номер объекта по условному номеру
Поиск в Росреестре по Адресу Потом «зеленки» были отменены. Сегодня строениям присваивается кадастровый номер, а основным документом, подтверждающим право собственности, является вписка из Единого государственного реестра недвижимости (ЕГРН).
Узнать кадастровый номер по условному можно только через отделения Росреестра. Сегодня проще всего узнать кадастровый номер по адресу. Сделать это можно бесплатно в режиме онлайн на сайте ЕГРН. Реестр.
Номер присваивался всем объектам недвижимости в частной собственности, отстроенным человеком, расположенным на территории РФ:
▪ В строке поиска введите адрес или кадастровый номер объекта и нажмите кнопку: Найти; Росреестр Найти Объект по Адресу
Условный номер: все о условном номере и его отличии от кадастрового
Поиск в Росреестре по Адресу Условный номер объекта недвижимости – уникальный набор чисел, присвоенный недвижимому имуществу до 2002 г.
После 2002 г недвижимости присваиваются кадастровые номера, а УНОН позволяет отследить юридические операции с ней до этого срока.
Данные о присвоенных недвижимости номерах хранит государственный орган Росреестр. Основные различия между нумерацией:
Номер присваивался всем объектам недвижимости в частной собственности, отстроенным человеком, расположенным на территории РФ.
Каким объектам может быть присвоен? (читать далее…)
Шифры состоят из чисел и дефисов между ними. Каждая группа чисел имеет определенное значение:
Поиск кадастрового номера по условному
Аналогичным способом работает сайт ЕГРНка. Для поиска данных о недвижимости можно использовать УНОН, указав его в одноименном поле. ЕГРНка выдаст подлинную, актуальную информацию о запрашиваемом недвижимом имуществе. Условный номер объекта недвижимости – что это такое?
Чем отличаются кадастровый и условный номера?
То, что его нет в документах не значит, что КНОН не присвоен недвижимости вообще.
Скорее всего, в Росреестре у недвижимости есть все необходимые значения и сведения. Проверить наличие КНОН можно одним из способов из предыдущего раздела статьи.
Шифр состоит из четырех групп чисел, разделенных двоеточиями. Последовательно значения числовых групп:
Структура кадастрового номера
Затем просто введите КНОН.
По сути, УНОН представляет собой порядковый номер регистрации конкретного объекта в регионе.
🟠 Заполните опросник и получите консультацию бесплатно
🟠 Все вопросы можно задать в форме ниже
🟠 Заполните опросник и получите консультацию бесплатно
🟠 Все вопросы можно задать в форме ниже
Поделиться
Класснуть
Поделиться
Загрузка…
Добавить комментарий
Почему полезно знать кадастровый номер объекта недвижимости?
Главная » Информация из Росреестра » Почему полезно знать кадастровый номер объекта недвижимости?
В нашей жизни каждый имеет документ, удостоверяющий личность, а приходя в магазин, на товарах мы видим маркировку.
Делается это для того, чтобы мы могли идентифицировать человека или, например, тот или иной товар. А как быть с объектами недвижимости? Мы имеем квартиры, дома, земельные участки и другие объекты недвижимости и у них также есть своя «маркировка».
Идентифицируются объекты недвижимости благодаря кадастровому номеру. Давайте рассмотрим, что такое кадастровый номер.
Каждый объект недвижимости, сведения о котором внесены в Единый государственный реестр недвижимости (ЕГРН), имеет неизменяемый, не повторяющийся во времени и на территории Российской Федерации кадастровый номер, присваиваемый органом регистрации прав единожды.
Благодаря этому в случаях, когда объекты имеют одинаковый адрес или повторяющиеся характеристики, мы всегда можем отличить один объект от другого.
Вам необходимо узнать площадь квартиры, вид разрешенного использования земельного участка, или какая категория земель у земельного участка. А может, вы хотите уточнить на каком этаже находится помещение.
Информация об объекте недвижимости может быть необходима перед покупкой недвижимости, чтобы убедиться в достоверности сведений.
Зная кадастровый номер объекта недвижимости, можно посмотреть нужную вам информацию, будь то жилой дом, земельный участок, квартира или сооружение.
У вас есть вопросы по имущественному налогу на объект недвижимости? Возник спорный вопрос по границам смежного земельного участка? Зная кадастровый номер, вы можете посмотреть информацию о кадастровой стоимости объекта, от которой исчисляется налог, или посмотреть расположение земельного участка на информационном ресурсе Росреестра «Публичная кадастровая карта».
Если есть кадастровый номер, значит объект стоит на учете и мы имеем возможность определить его точное месторасположение, посмотреть характеристики объекта и уточнить кто является его правообладателем.
Если сведения об объекте недвижимости отсутствуют в ЕГРН и объекту не присвоен кадастровый номер, то с ним невозможно совершить сделку и зарегистрировать своё право в органе регистрации прав.
А это значит, что распорядиться своим имуществом будет невозможно.
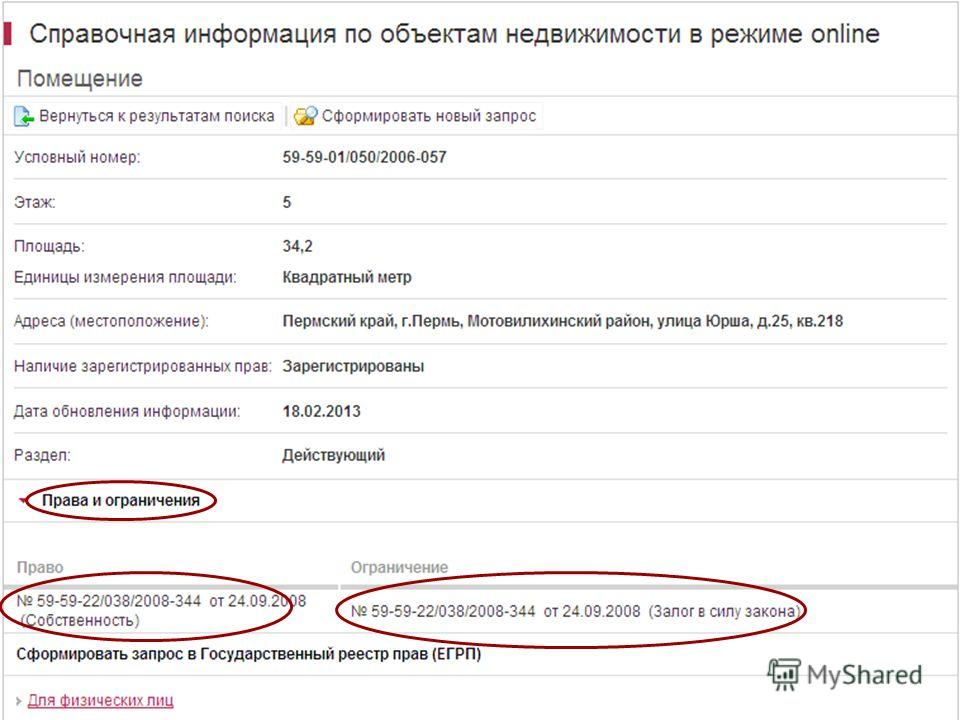
Что делать тем, кто не знает какой кадастровый номер у объекта недвижимости? И как узнать, содержатся ли сведения об этом объекте в ЕГРН?
Зная адрес объекта недвижимости или его условный номер, любой желающий сможет найти свою недвижимость и узнать кадастровый номер на официальном сайте Росреестра в сети Интернет: https://rosreestr.ru/, воспользовавшись сервисом «Справочная информация по объектам недвижимости в режиме online».
Вы нашли свой объект, значит, сведения о нем содержатся в ЕГРН. Если сведения отсутствуют, то вы вправе обратиться с соответствующим заявлением в многофункциональный центр. К заявлению необходимо приложить правоустанавливающие или правоудостоверяющие документы на объект недвижимости.
В случае наличия в указанных документах необходимой информации, сведения об объекте будут внесены в ЕГРН и объекту присвоен кадастровый номер.
линейная алгебра — Номер условия произведения двух матриц
спросил
Изменено 1 год, 10 месяцев назад
Просмотрено 9к раз
$\begingroup$
Для двух квадратных матриц $A$ и $B$ выполняется следующее неравенство
$$\operatorname{cond}(AB) \leq \operatorname{cond}(A)\operatorname{cond}(B),$$, где $\operatorname {cond}$ — номер условия, верно? 9{-1}$ не имеет смысла, и номер условия должен быть определен по-другому.
Единственное определение, которое я знаю для этого случая (которое согласуется с приведенным выше, когда используется операторная норма), это
$$
\operatorname{cond}(A)=\frac{\sigma_1(A)}{\sigma_n(A)} = \frac{\max\{|Ax|:|x|=1\}}{\min \{ |Топор| : |х|=1\}}
$$
(Здесь $\sigma_1$ и $\sigma_n$ — наибольшее и наименьшее сингулярные значения $A$, определенные в частном справа).
Это определение представляет интерес только тогда, когда ядро тривиально. Субмультипликативное неравенство остается в силе, так как $\sigma_1(AB)\le \sigma_1(A)\sigma_1(B)$ и $\sigma_n(AB)\ge \sigma_n(A)\sigma_n(B) $.
$\endgroup$
3
$\begingroup$
Я хотел бы немного пояснить: рассуждения в ответе пользователя 103402 не совсем ясны в случае, когда матрицы не квадратные, и это может заставить вас думать, что что-то ложное является правдой, как показано в ответе loup blanc.
$
\newcommand{\sig}{\operatorname{\sigma}}
\ новая команда {\ R} {\ mathbb R}
\newcommand{\norm}[1]{\lVert #1 \rVert}
$ 9{n \раз p}$.
Тогда вопрос становится
$$
\operatorname{cond}(AB) = \frac{\sig_1(AB)}{\sig_{\min(m,p)}(AB)}
\ stackrel {?} {\ le} \ frac {\ sig_1 (A)} {\ sig _ {\ min (m, n)} (A)} \ frac {\ sig_1 (B)} {\ sig _ {\ min ( n,p)}(B)} = \operatorname{cond}(A) \operatorname{cond}(B)
.$$
$\sig_1(AB) \le \sig_1(A) \sig_1(B)$ выполняется всегда; вопрос в том,
$$
\sig_{\min(m,p)}(AB) \stackrel{?}{\ge} \sig_{\min(m,n)}(A) \sig_{\min(n,p)}(B )
.$$
Если предположить, что $m \ge n \ge p$, то это верно. Мы можем видеть это, потому что: 9+||=1/\sigma_k$ и (относительно определения выше) $cond(U)=\sigma_1/\sigma_k$.
Контрпример к $n\not= p,A\in M_{n,p},B\in M_{p,n},cond(AB)\leq cond(A)cond(B)$.
Возьмите $n=2,p=4$ и $A=\begin{pmatrix}99&-95.001&-25&76\\99&-95&-25&76\end{pmatrix},B=\begin{pmatrix}10&-62 \\-44&-83\\26&9\\-3&88\end{pmatrix}$.
Обратите внимание, что $A$ плохо обусловлен.
Подробнее см. мой ответ в
Контрпример или доказательство того, что $\kappa(AB) \leq \kappa(A)\kappa(B) $
$\endgroup$
Что такое номер состояния матрицы? » Cleve’s Corner: Cleve Moler on Mathematics and Computing
Несколько вопросов в комментариях к недавним сообщениям в блоге побудили меня обсудить матричные числа условий.
В комментарии к моему посту о матрицах Гильберта читатель по имени Мишель спросил:
- Можете ли вы прокомментировать, когда число обусловленности дает точную оценку ошибки в вычисляемой обратной величине и существует ли лучшая оценка?
В комментарии к моему сообщению о четверной точности Марк спросил:
- У вас есть какое-нибудь представление о коэффициенте замедления… для решения больших линейных уравнений с крайне плохо обусловленными матрицами?
Мои краткие ответы заключаются в том, что оценка погрешности редко бывает точной, но невозможно найти лучшую, и что для решения плохо обусловленных линейных уравнений требуется столько же времени, сколько и для решения правильных уравнений.
кондиционированные системы.
Содержание
- Номер условия для инверсии
- Нормы
- Линейные уравнения
- Пример
- Близко к единственному числу
- . что, хотя спрашивающие, возможно, не понимали этого, они спрашивали только об одном из них — числе условий для инверсии. В общем случае число обусловленности относится не только к конкретной матрице, но и к решаемой задаче. Инвертируем ли мы матрицу, находим ее собственные значения или вычисляем экспоненту? Список можно продолжить. Матрица может быть плохо обусловлена для обращения, в то время как проблема собственных значений хорошо обусловлена. Или наоборот.
Число условия для матричной и вычислительной задачи измеряет, насколько чувствителен ответ к возмущениям во входных данных и к ошибкам округления, допущенным в процессе решения.
Когда мы просто говорим, что матрица «плохо обусловлена», мы обычно думаем только о чувствительности ее инверсии, а не обо всех других числах обусловленности.
Нормы
Чтобы уточнить эти понятия, начнем с векторной нормы. В частности, евклидова норма 9{1/2}$$
Это расстояние «по прямой» в n -мерном пространстве.
Соответствующая норма матрицы $A$ измеряет, насколько отображение, индуцированное этой матрицей, может растягивать векторы.
$$M \ = \\|A\| \ = \ {\max {{\|Ax\|} \over {\|x\|}}}$$
Иногда также важно учитывать, насколько матрица может сжимать векторы.
$$m \ = \ {\min {{\|Ax\|} \over {\|x\|}}}$$
Обратная величина минимального растяжения является нормой обратной, поскольку 9{-1}\|$$
Если матрица вырожденная, то ее число обусловленности бесконечно.
Линейные уравнения
Число обусловленности $\kappa(A)$ участвует в ответе на вопрос: Насколько изменение правой части системы одновременных линейных уравнений может повлиять на решение? Рассмотрим систему уравнений
$$A x \ = \ b$$
и вторую систему, полученную изменением правой части
$$A(x + \delta x) = b + \delta b$ $
Думайте о $\delta b$ как об ошибке в $b$, а $\delta x$ как о результирующей ошибке в $x$, хотя нам не нужно делать никаких предположений о том, что ошибки малы.
Поскольку $A (\delta x) = \delta b$, определения $M$ и $m$ немедленно приводят к$$\|b\| \leq M \|x\|$$
и
$$\|\delta b\| \geq m \|\delta x\|$
Следовательно, если $m \neq 0$,
$${\|\delta x\| \over \|x\|} \leq \kappa(A) {\|\delta b\| \над \|b\|}$$
Величина $\|\delta b\|/\|b\|$ представляет собой относительное изменение в правой части, а величина $\|\delta x\|/\|x\|$ равна в результате относительных изменений в растворе. Преимущество использования относительных изменений состоит в том, что они
Это неравенство показывает, что число обусловленности является коэффициентом увеличения относительной ошибки. Изменения в правой части могут вызвать изменения решения в $\kappa(A)$ раза больше.
Пример
Исследуем систему линейных уравнений, включающую
$$A=\left(\begin{array}{cc} 4.1 & 2.8 \\ 9.7 & 6.6 \end{array}\right)$$
Возьмем $b$ за первый столбец $A$, поэтому решение $Ax = b$ будет просто
$$x = \left(\begin{array}{c} 1 \\ 0 \end{array }\right)$$
Переключиться на MATLAB
A = [4.
1 2.8; 9,7 6,6]
б = А (:, 1)
х = А\б
А = 4.1000 2.8000 9.7000 6.6000 б = 4.1000 9.7000 х = 1.0000 -0,0000Теперь добавьте 0,01 к первому компоненту b.
b2 = [4,11; 9.7]
б2 = 4.1100 9.7000Решение резко меняется.
х2 = А\b2
х2 = 0,3400 0,9700Эта чувствительность решения x к изменениям в правой части b является отражением числа обусловленности.
каппа = условный (А)
каппа = 1.6230e+03
Верхняя граница возможного изменения x указывает на изменения всех значащих цифр.
каппа*норма(b-b2)/норма(b)
и = 1,5412Фактическое изменение x в результате этого возмущения равно
норма(х-х2)/норма(х)
и = 1.1732Таким образом, это конкретное изменение в правой части привело к почти самому большому возможному изменению решения.
Близко к сингулярности
Большое число обусловленности означает, что матрица близка к сингулярности. Сделаем небольшое изменение во втором ряду A.
A А2 = [4,1 2,8; 9,676 6,608]
А = 4.1000 2.8000 9,7000 6,6000 А2 = 4.1000 2.8000 9,6760 6,6080Результирующая матрица эффективно сингулярна. Если мы попытаемся вычислить его инверсию, мы получим предупреждающее сообщение.
A2инв = инв(A2)
Предупреждение. Матрица близка к единственной или плохо масштабируется. Результаты могут быть неточными. RCOND = 1,988677e-17. A2инв = 1.0e+15 * -1,4812 0,6276 2,1689 -0,9190Величина RCOND в предупреждении является оценкой обратной величины номера условия. Использование обратного числа осталось со времен, когда у нас не было арифметики с плавающей запятой IEEE с Inf для представления переполнения и бесконечности. Для этого примера RCOND имеет порядок eps(1), а коэффициент масштабирования для A2inv означает, что его элементы бесполезны.
Невозможно вычислить то, чего нет. 9{-1}\|}} \\le\
\kappa(A) {{\|E\|} \over {\|A\|}}$$Работа Джима Уилкинсона об ошибке округления в методе исключения Гаусса показала, что каждый столбец вычисляемой обратной функции является столбцом точной обратная матрица в пределах ошибки округления данной матрицы. Давайте немного схитрим и скажем, что inv(A) вычисляет точную обратную величину $A+E$, где $\|E\|$ имеет порядок ошибки округления по сравнению с $\|A\|$ .
Мы не знаем точно $E$, но для матрицы размера n на n мы имеем оценку
norm(E) $\приблизительно \space$ n*eps(norm(A))
Итак, у нас есть простая оценка ошибки в вычисленном обратном значении относительно неизвестного точного обратного.
X = $\space$ точная инверсия A
Z = inv(A)
норма(Z — X)/норма(X) $\приблизительно$ n*eps*cond(A)
Для нашего 2 Пример — на 2 оценка относительной ошибки в вычисленном обратном значении равна
2*eps*condest(A)
и = 9.
9893e-13
Это говорит о том, что мы можем ожидать 12 или 13 (из 16) значащих цифр.
Уилкинсон должен был предположить, что каждая отдельная арифметическая операция с плавающей запятой вызывает максимальную ошибку округления. Но только часть операций вообще имеет какую-либо ошибку округления, и даже для них ошибки меньше максимально возможного. Так что эту оценку можно ожидать завышенной. Но более точная оценка невозможна.
Для нашего примера вычисленная инверсия имеет формат
Z = инв (А)
З = -66.000000000000057 28.000000000000025 97.000000000000085 -41.000000000000036
Оказывается, точная инверсия имеет целочисленные записи, полученные с помощью
X = round(Z)
Х = -66 28 97 -41Мы можем сравнить фактическую относительную ошибку с оценкой.
формат короткий норма(Z - X)/норма(X)
и = 8.7342э-16
Таким образом, мы имеем более 15 значащих цифр точности.
Поскольку $A (\delta x) = \delta b$, определения $M$ и $m$ немедленно приводят к
1 2.8; 9,7 6,6]
б = А (:, 1)
х = А\б
Невозможно вычислить то, чего нет. 9{-1}\|}} \\le\
\kappa(A) {{\|E\|} \over {\|A\|}}$$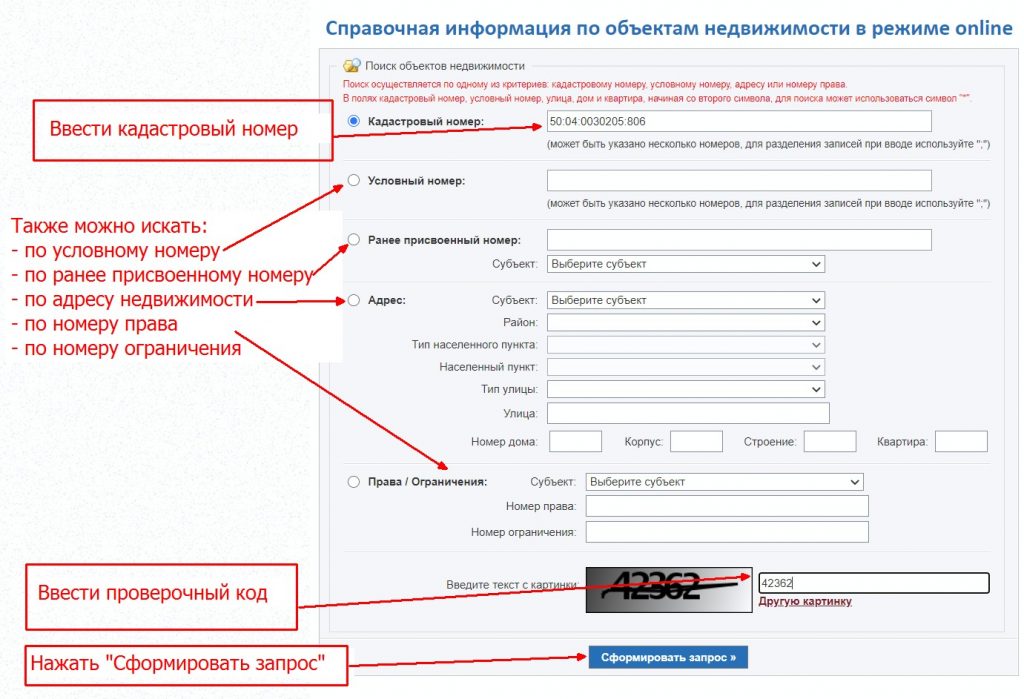
9893e-13
