Статья 144 Семейного кодекса РФ в новой редакции с Комментариями и последними поправками на 2022 год
Новая редакция Ст. 144 СК РФ
Отмена усыновления ребенка не допускается, если к моменту предъявления требования об отмене усыновления усыновленный ребенок достиг совершеннолетия, за исключением случаев, когда на такую отмену имеется взаимное согласие усыновителя и усыновленного ребенка, а также родителей усыновленного ребенка, если они живы, не лишены родительских прав или не признаны судом недееспособными.
Комментарий к Статье 144 СК РФ
По общему правилу отмена усыновления допускается только до достижения ребенком совершеннолетия. Изъятия из этого правила составляют случаи, когда отмена усыновления совершеннолетнего лица допускается по взаимному согласию усыновителя и усыновленного ребенка, а также родителей усыновленного ребенка, если они живы, не лишены родительских прав и не признаны судом недееспособными.
Как было отмечено в Определении Конституционного Суда РФ от 17 декабря 2008 г. N 1055-О-П, положения статьи 144 СК в системе действующего правового регулирования не предполагают отказ по причине несогласия усыновителя в удовлетворении требования об отмене усыновления достигшему совершеннолетия усыновленному, в отношении которого усыновителем было совершено преступление против половой неприкосновенности несовершеннолетнего.
N 1055-О-П, положения статьи 144 СК в системе действующего правового регулирования не предполагают отказ по причине несогласия усыновителя в удовлетворении требования об отмене усыновления достигшему совершеннолетия усыновленному, в отношении которого усыновителем было совершено преступление против половой неприкосновенности несовершеннолетнего.
Из этой весьма витиеватой формулировки Конституционного Суда следует, что в подобных случаях усыновление может быть отменено и в отношении совершеннолетнего лица, даже если усыновитель возражает против такой отмены.
Другой комментарий к Ст. 144 Семейного кодекса Российской Федерации
1. Отмена усыновления в соответствии со ст.144 СК РФ не допускается, если ко времени подачи искового заявления усыновленный достиг возраста 18 лет, за исключением случаев, когда на отмену усыновления имеется взаимное согласие усыновителя и совершеннолетнего усыновленного, а также его родителей, если они живы, не лишены родительских прав или не признаны судом недееспособными.
2. СК РФ в отличие от КоБС (ст.112) не предусматривает оснований для признания усыновления недействительным. Учитывая это, суд вправе признать недействительным на основании ст.112 КоБС усыновление, произведенное до введения в действие СК РФ в случае, когда решение об усыновлении было основано на подложных документах или когда усыновителем являлось лицо, лишенное родительских прав либо признанное в установленном законом порядке недееспособным или ограниченно дееспособным, а также при фиктивности усыновления.
Усыновление, произведенное с указанными выше нарушениями после введения в действие СК РФ, но до введения в действие судебного порядка усыновления (т.е. с 1 марта по 26 сентября 1996 г.), может быть признано судом недействительным, если это отвечает интересам ребенка. Если указанные нарушения были допущены при усыновлении ребенка в судебном порядке, то они могут явиться основанием к отмене судебного решения и отказу в удовлетворении заявления об усыновлении, а не для признания усыновления недействительным. Этот вопрос также решается судом исходя из интересов ребенка.
Этот вопрос также решается судом исходя из интересов ребенка.
Ст. 144 СК РФ с Комментариями 2021-2022 года (новая редакция с последними изменениями)
Отмена усыновления ребенка не допускается, если к моменту предъявления требования об отмене усыновления усыновленный ребенок достиг совершеннолетия, за исключением случаев, когда на такую отмену имеется взаимное согласие усыновителя и усыновленного ребенка, а также родителей усыновленного ребенка, если они живы, не лишены родительских прав или не признаны судом недееспособными.
1. В соответствии с комментируемой статьей отмена усыновления — это судебная процедура, проведение которой допускается по общему правилу до достижения ребенком совершеннолетия. Исковое заявление об отмене усыновления, как следует из текста комментируемой статьи, должно быть заявлено до исполнения ребенку 18 лет.
Вместе с тем комментируемая статья предусматривает одно исключение из этого правила. При наличии таких условий, как: 1) взаимное согласие на отмену усыновления усыновителя и усыновленного ребенка, а также родителей усыновленного ребенка; 2) наличие в живых родителей усыновленного ребенка, которые ранее не были лишены родительских прав и не были признаны судом недееспособными на момент предъявления иска, отмена усыновления возможна и в отношении совершеннолетнего усыновленного.
Бесплатная юридическая консультация по телефонам:
8 (499) 938-53-89 (Москва и МО)
8 (812) 467-95-35 (Санкт-Петербург и ЛО)
8 (800) 302-76-91 (Регионы РФ)
Эти случаи действительно исключительны.
Особенность процедуры отмены усыновления в этом случае состоит в том, что возможные ответчики по иску заранее с иском согласны. Между тем законодательство не предусматривает иной специальной, в том числе внесудебной, процедуры отмены усыновления для такого случая.
2. Положения комментируемой статьи были проанализированы Конституционным Судом РФ по заявлению гражданки Ф., 1978 года рождения . Она была удочерена отчимом с присвоением ей его фамилии и отчества. В 2007 г. Ф. обратилась в суд общей юрисдикции с заявлением об отмене удочерения, в котором в обоснование своих требований ссылалась на ст. 141 СК РФ, допускающую отмену усыновления в случаях жестокого обращения усыновителя с усыновленным, и на приговор суда, которым ее отчим был осужден за совершение в отношении ее преступления, предусмотренного ч. 3 ст. 117 УК РСФСР (изнасилование несовершеннолетней), к пяти годам лишения свободы. Решением суда первой инстанции, оставленным без изменения судом кассационной инстанции, Ф. было отказано в удовлетворении ее исковых требований со ссылкой на то, что даже при наличии установленных ст. 141 СК РФ оснований для отмены удочерения положения комментируемой статьи не позволяют удовлетворить требования достигшей совершеннолетия истицы без согласия усыновителя.
3 ст. 117 УК РСФСР (изнасилование несовершеннолетней), к пяти годам лишения свободы. Решением суда первой инстанции, оставленным без изменения судом кассационной инстанции, Ф. было отказано в удовлетворении ее исковых требований со ссылкой на то, что даже при наличии установленных ст. 141 СК РФ оснований для отмены удочерения положения комментируемой статьи не позволяют удовлетворить требования достигшей совершеннолетия истицы без согласия усыновителя.
———————————
Определение Конституционного Суда РФ от 17 декабря 2008 г. N 1055-О-П «По жалобе гражданки Ф. на нарушение ее конституционных прав статьей 144 Семейного кодекса Российской Федерации».
По мнению Ф., комментируемая статья не соответствует Конституции РФ, ее ст. ст. 2, 15, 23 и 60, поскольку закрепленное ею условие отмены усыновления при наличии законных оснований — согласия усыновителя — по достижении ребенком совершеннолетия влечет недопустимое в правовом государстве ограничение конституционных прав усыновленного, в отношении которого усыновителем совершено преступление.
Как отметил Конституционный Суд РФ в своем Определении по данному заявлению, положения комментируемой статьи в системе действующего правового регулирования не предполагают отказ — по причине несогласия усыновителя — в удовлетворении требования об отмене усыновления достигшему совершеннолетия усыновленному, в отношении которого усыновителем было совершено преступление против половой неприкосновенности несовершеннолетнего.
skrf.media.mline — scikit-rf Документация
"""
MLine (:mod:`skrf.media.MLine`)
========================================
.. автосуммирование::
:toctree: сгенерировано/
МЛиния
"""
импортировать numpy как npy
из журнала импорта numpy, log10, tanh, sqrt, exp, real, imag, cosh, \
единицы, нули, арктангенс
из scipy.constants импортировать epsilon_0, mu_0, c, pi
из .media импорт Медиа
из ..tlineFunctions импортировать skin_depth, surface_resistivity
из ..констант импортировать NumberLike
набрав import Union, TYPE_CHECKING
предупреждения об импорте
если TYPE_CHECKING:
из . . частота импорт Частота
. частота импорт Частота
[документы]класс MLine(Media):
р"""
Микрополосковая линия передачи, определяемая по ширине, толщине
и высота на заданной подложке относительной диэлектрической проницаемости. В линии есть
удельное сопротивление проводника и коэффициент тангенциальных потерь.
Этот класс вдохновлен технической документацией [#]_
и исходники, предоставленные проектом qucs [#]_ .
Кроме того, Джорджевич [#]_ /Свенсон [#]_ широкополосный диэлектрик Дебая
Считается, что эта модель обеспечивает более реалистичное моделирование широкополосной связи.
микрополоска с причинно-следственным откликом во временной области.
Предусмотрен режим совместимости, имитирующий поведение QUCS или
ADS компании Keysight. Существуют известные различия в выходе этих
тренажеры.
Квазистатические модели херкеристического импеданса и эффективного
диэлектрическая проницаемость дает значение при нулевой частоте. Дисперсионные модели
вычислить частотно-зависимые значения этих переменных.
* Модели квазистатического волнового сопротивления и эффективной диэлектрической проницаемости:
+ Хаммерстад и Дженсен (по умолчанию)
+ Шнайдер
+ Уилер
* Частотная дисперсия моделей импеданса и эффективной диэлектрической проницаемости:
+ Хаммерстад и Дженсен
+ Киршнинг и Янсен (по умолчанию)
+ Кобаяши
+ Шнайдер
+ Ямасита
+ (без дисперсии)
* Модель коррекции толщины полосы:
+ все квазистатические модели добавляют определенную величину к W для учета
ненулевая толщина полосы. Расчет с нулевой толщиной
возможный.
Параметры
----------
частота : :класс:`~skrf.frequency.Frequency` объект
полоса частот носителя
z0 : число, массив или None
импеданс порта для среды. Требуется только в том случае, если отличается от
волновое сопротивление Z0 линии передачи. в омах
w : число или массив
ширина проводника, м
h : число или массив
высота подложки между плоскостью заземления и проводником, м
t : число, или массив, или None, необязательный
толщина проводника, м. По умолчанию — None (без коррекции ширины).
с учетом толщины полосы).
ep_r : число или массив
относительная диэлектрическая проницаемость диэлектрика на частоте f_epr_tand, ед.
mu_r : число, подобное массиву
относительная проницаемость мд диэлектрика, шт.
модель : ул.
микрополосковый квазистатический импеданс и диэлектрическая модель в:
* 'хаммерстадженсен' (по умолчанию)
* 'Шнайдер'
* 'Уилер'
дисп : ул
модель микрополоскового импеданса и диэлектрической частотной дисперсии в:
* 'хаммерстадженсен'
* 'киршнингянсен' (по умолчанию)
* 'кобаяси'
* 'Шнайдер'
* 'ямасита'
* 'никто'
номер : ул.
модель дисперсии диэлектрической частоты в:
* 'джорджевичсвенссон' (по умолчанию)
* 'частотно-инвариантный'
ро: число или массив, необязательно
Удельное сопротивление проводника, Ом/м
tand : число или массив
Коэффициент диэлектрических потерь на частоте f_epr_tand
rough : число или массив
Среднеквадратическая шероховатость проводника в м
f_low : число или массив
более низкая частота для широкополосного диэлектрика Дебая Джорджевича/Свенсона
модель, в Гц
f_high : число или массив
более высокая частота для широкополосного диэлектрика Дебая Джорджевича / Свенссона
модель, в Гц
f_epr_tand : число или массив
частота измерения ep_r и tand диэлектрика, Гц
compatibility_mode: str или None (по умолчанию)
Если установлено значение «qucs», происходит следующее поведение:
* Волновое сопротивление будет действительным (без мнимой части из-за tand)
* Квазистатические относительные диэлектрическая проницаемость и импеданс будут использоваться для
расчет потерь вместо частотно-дисперсионных значений
* Модели Кобаяши и Ямасита рассеивают диэлектрическую проницаемость, но сохраняют
значения квазистатического импеданса
\*args, \*\*kwargs : аргументы, аргументы ключевого слова
передается в конструктор :class:`~skrf.
По умолчанию — None (без коррекции ширины).
с учетом толщины полосы).
ep_r : число или массив
относительная диэлектрическая проницаемость диэлектрика на частоте f_epr_tand, ед.
mu_r : число, подобное массиву
относительная проницаемость мд диэлектрика, шт.
модель : ул.
микрополосковый квазистатический импеданс и диэлектрическая модель в:
* 'хаммерстадженсен' (по умолчанию)
* 'Шнайдер'
* 'Уилер'
дисп : ул
модель микрополоскового импеданса и диэлектрической частотной дисперсии в:
* 'хаммерстадженсен'
* 'киршнингянсен' (по умолчанию)
* 'кобаяси'
* 'Шнайдер'
* 'ямасита'
* 'никто'
номер : ул.
модель дисперсии диэлектрической частоты в:
* 'джорджевичсвенссон' (по умолчанию)
* 'частотно-инвариантный'
ро: число или массив, необязательно
Удельное сопротивление проводника, Ом/м
tand : число или массив
Коэффициент диэлектрических потерь на частоте f_epr_tand
rough : число или массив
Среднеквадратическая шероховатость проводника в м
f_low : число или массив
более низкая частота для широкополосного диэлектрика Дебая Джорджевича/Свенсона
модель, в Гц
f_high : число или массив
более высокая частота для широкополосного диэлектрика Дебая Джорджевича / Свенссона
модель, в Гц
f_epr_tand : число или массив
частота измерения ep_r и tand диэлектрика, Гц
compatibility_mode: str или None (по умолчанию)
Если установлено значение «qucs», происходит следующее поведение:
* Волновое сопротивление будет действительным (без мнимой части из-за tand)
* Квазистатические относительные диэлектрическая проницаемость и импеданс будут использоваться для
расчет потерь вместо частотно-дисперсионных значений
* Модели Кобаяши и Ямасита рассеивают диэлектрическую проницаемость, но сохраняют
значения квазистатического импеданса
\*args, \*\*kwargs : аргументы, аргументы ключевого слова
передается в конструктор :class:`~skrf.
media.media.Media`
(:func:`~skrf.media.media.Media.__init__`
Примечание
----
В случае, когда дисперсионная модель включает только эффективную диэлектрическую проницаемость, нет
дисперсия используется для импеданса в режиме QUCS, а Киршнинг Янсен
используется в режиме ADS. Режим QUCS используется по умолчанию.
При толщине полосы менее 3 толщин скин-слоя потери
модель дает чрезмерно оптимистичные результаты, и средства массовой информации вынесут предупреждение.
При постоянном токе потери в линии могут быть меньше, чем в ее проводнике.
сопротивление, которое не является физическим.
использованная литература
----------
.. [#] http://qucs.sourceforge.net/docs/technical.pdf
.. [#] https://github.com/Qucs/qucsator/blob/develop/src/components/microstrip/msline.cpp
.. [#] Э. Хаммерстад и Ø. Дженсен,
«Точные модели для автоматизированного проектирования микрополосковых полос»,
Симпозиум по теории и технике микроволнового излучения, стр. 407-409., июнь 1980 г.
.. [#] М. Киршнинг и Р. Х. Янсен,
"Точная модель эффективной диэлектрической проницаемости микрополосковой полосы с
Действительность до частот миллиметрового диапазона », Electronics Letters,
об. 8, нет. 6, стр. 272-273, март 1982 г.
.. [#] Р. Х. Янсен и М. Киршнинг,
«Аргументы и точная модель силовой токовой формулировки
Характеристическое сопротивление микрополосковой полосы",
Archiv für Elektronik und Übertragungstechnik (AEÜ), vol. 37,
стр. 108-112, 1983.
.. [#] М. Кобаяши,
«Формула дисперсии, отвечающая последним требованиям к микрополосковым технологиям».
CAD", IEEE Trans. on Microwave Theory and Techniques, т. 36, № 8,
стр. 1246-1250, август 1988 г.
.. [#] М. В. Шнейдер,
"Микрополосковые линии для интегральных микросхем СВЧ",
Технический журнал Bell System, vol. 48, стр. 1421-1444, май 1969 г.
.. [#] М. В. Шнайдер, «Микрополосковая дисперсия», Труды IEEE,
Письма, том.
407-409., июнь 1980 г.
.. [#] М. Киршнинг и Р. Х. Янсен,
"Точная модель эффективной диэлектрической проницаемости микрополосковой полосы с
Действительность до частот миллиметрового диапазона », Electronics Letters,
об. 8, нет. 6, стр. 272-273, март 1982 г.
.. [#] Р. Х. Янсен и М. Киршнинг,
«Аргументы и точная модель силовой токовой формулировки
Характеристическое сопротивление микрополосковой полосы",
Archiv für Elektronik und Übertragungstechnik (AEÜ), vol. 37,
стр. 108-112, 1983.
.. [#] М. Кобаяши,
«Формула дисперсии, отвечающая последним требованиям к микрополосковым технологиям».
CAD", IEEE Trans. on Microwave Theory and Techniques, т. 36, № 8,
стр. 1246-1250, август 1988 г.
.. [#] М. В. Шнейдер,
"Микрополосковые линии для интегральных микросхем СВЧ",
Технический журнал Bell System, vol. 48, стр. 1421-1444, май 1969 г.
.. [#] М. В. Шнайдер, «Микрополосковая дисперсия», Труды IEEE,
Письма, том.
60, январь 1972 г., стр. 144–146.
.. [#] Х. А. Уиллер,
«Свойства линии передачи полосы на диэлектрическом листе на
Самолет, IEEE Trans. по теории и технике микроволнового излучения, т. 1, с. 25, нет. 8,
стр. 631-647, 19 августа.77.
.. [#] H.A. Wheeler, «Формулы скин-эффекта»,
Труды IRE, vol. 30, нет. 9, стр. 412-424, сентябрь 1942 г.
.. [#] Э. Ямасита, К. Ацуки и Т. Уэда,
"Приблизительная формула дисперсии микрополосковых линий для ЭВМ".
Aided Design of Microwave Integrated Circuits », IEEE Trans. on
Теория и методы микроволнового излучения, том. 27, стр. 1036-1038, декабрь 1979 г.
.. [#] К. Свенссон, Г.Е. Дермер,
Моделирование межсоединений с потерями во временной области,
IEEE транс. по усовершенствованной упаковке, май 2001 г., N2, Vol. 24, стр. 191-196.
.. [#] Джорджевич, Р.М. Билич, В.Д. Ликар-Смилянич, Т.К. Саркар,
Широкополосная характеристика FR-4 в частотной области и во временной области
причинность,
IEEE транс. по ЭМС, вып. 43, №4, 2001, с. 662-667.
"""
по ЭМС, вып. 43, №4, 2001, с. 662-667.
"""
[документы] def __init__(self, Frequency: Union['Frequency', None] = None,
z0: Union[NumberLike, None] = Нет,
w: NumberLike = 3, h: NumberLike = 1,6,
t: Union[NumberLike, None] = Нет,
ep_r: NumberLike = 4,5,
mu_r: NumberLike = 1,0,
модель: str = 'hammerstadjensen',
disp: ул = 'киршнингянсен',
diel: str = 'djordjevicsvensson',
ро: NumberLike = 1.68e-8, tand: NumberLike = 0,
грубо: NumberLike = 0,15e-6,
f_low: NumberLike = 1e3, f_high: NumberLike = 1e12,
f_epr_tand: NumberLike = 1e9,
compatibility_mode: Union[str, None] = None,
*args, **kwargs):
Media.__init__(я, частота = частота, z0 = z0)
self.w, self.h, self.t = w, h, t
self.ep_r, self.mu_r = ep_r, mu_r
self.
model, self.disp, self.diel = модель, дисп, дизель
self.rho, self.tand, self.rough, self.disp = rho, tand, грубый, disp
self.f_low, self.f_high, self.f_epr_tand = f_low, f_high, f_epr_tand
self.compatibility_mode = режим_совместимости
# изменение эффективной диэлектрической проницаемости в зависимости от частоты
# Не реализовано в QUCS, но реализовано в ADS.
# 'частотный инвариант' даст постоянное комплексное значение с реальным
# часть, совместимая с qucs, и мнимая часть из-за tand
self.ep_r_f, self.tand_f = self.analyse_dielectric(
self.ep_r, self.tand,
self.f_low, self.f_high, self.f_epr_tand, self.frequency.f,
селф.диэль)
# квазистатическая эффективная диэлектрическая проницаемость подложки + линии и
# импеданс микрополосковой линии
# qucs использует ep_r с действительным знаком, что дает импеданс с действительным знаком
если compatibility_mode == 'qucs':
self. zl_eff, self.ep_reff, self.w_eff = self.analyse_quasi_static(
реальный (self.ep_r_f), self.w, self.h, self.t, self.model)
# в объявлениях используется комплексная диэлектрическая проницаемость, дающая комплексный импеданс и
# эффективная диэлектрическая проницаемость
еще:
self.zl_eff, self.ep_reff, self.w_eff = self.analyse_quasi_static(
self.ep_r_f, self.w, self.h, self.t, self.model)
# анализировать дисперсию импеданса и относительной диэлектрической проницаемости
# qucs использует w здесь, но w_eff кажется лучше
если compatibility_mode == 'qucs':
self._z_characteristic, self.ep_reff_f = self.analyse_дисперсия(
self.zl_eff, self.ep_reff, реальный (self.ep_r_f),
self.w, self.w_eff, self.h, self.t,
собственная частота.f, собственный дисплей)
еще:
self._z_characteristic, self.ep_reff_f = self.analyse_дисперсия(
self.
zl_eff, self.ep_reff, self.w_eff = self.analyse_quasi_static(
реальный (self.ep_r_f), self.w, self.h, self.t, self.model)
# в объявлениях используется комплексная диэлектрическая проницаемость, дающая комплексный импеданс и
# эффективная диэлектрическая проницаемость
еще:
self.zl_eff, self.ep_reff, self.w_eff = self.analyse_quasi_static(
self.ep_r_f, self.w, self.h, self.t, self.model)
# анализировать дисперсию импеданса и относительной диэлектрической проницаемости
# qucs использует w здесь, но w_eff кажется лучше
если compatibility_mode == 'qucs':
self._z_characteristic, self.ep_reff_f = self.analyse_дисперсия(
self.zl_eff, self.ep_reff, реальный (self.ep_r_f),
self.w, self.w_eff, self.h, self.t,
собственная частота.f, собственный дисплей)
еще:
self._z_characteristic, self.ep_reff_f = self.analyse_дисперсия(
self. zl_eff, self.ep_reff, self.ep_r_f,
self.w_eff, self.w_eff, self.h, self.t,
собственная частота.f, собственный дисплей)
# анализируем потери линии
# qucs использует здесь квазистатические значения, что приводит к разнице
# против рекламы
если compatibility_mode == 'qucs':
self.alpha_conductor, self.alpha_dielectric = self.analyse_loss(
реальный (self.ep_r_f), реальный (self.ep_reff), self.tand_f,
self.rho, self.mu_r,
реальный (self.zl_eff), реальный (self.zl_eff),
self.frequency.f, self.w, self.t, self.rough)
еще:
self.alpha_conductor, self.alpha_dielectric = self.analyse_loss(
реальный (self.ep_r_f), реальный (self.ep_reff_f), self.tand_f,
self.rho, self.mu_r,
реальный (self._z_characteristic), реальный (self._z_characteristic),
self.frequency.f, self.w, self.
zl_eff, self.ep_reff, self.ep_r_f,
self.w_eff, self.w_eff, self.h, self.t,
собственная частота.f, собственный дисплей)
# анализируем потери линии
# qucs использует здесь квазистатические значения, что приводит к разнице
# против рекламы
если compatibility_mode == 'qucs':
self.alpha_conductor, self.alpha_dielectric = self.analyse_loss(
реальный (self.ep_r_f), реальный (self.ep_reff), self.tand_f,
self.rho, self.mu_r,
реальный (self.zl_eff), реальный (self.zl_eff),
self.frequency.f, self.w, self.t, self.rough)
еще:
self.alpha_conductor, self.alpha_dielectric = self.analyse_loss(
реальный (self.ep_r_f), реальный (self.ep_reff_f), self.tand_f,
self.rho, self.mu_r,
реальный (self._z_characteristic), реальный (self._z_characteristic),
self.frequency.f, self.w, self. t, self.rough)
t, self.rough)
def __str__(я) -> ул:
f=собственная частота
вывод = \
«Микрополосковые СМИ. %i-%i %s. %i очков'%\
(f.f_scaled[0],f.f_scaled[-1],f.unit, f.npoints) + \
'\n W= %.2em, H= %.2em'% \
(я.ш, я.ч)
возвратный вывод
def __repr__(self) -> ул:
вернуть себя.__str__()
@имущество
гамма по определению (я):
"""
Постоянная распространения.
Возвращает
-------
гамма: :класс:`numpy.ndarray`
"""
ep_reff, f = реальный (self.ep_reff_f), self.frequency.f
альфа = self.alpha_dielectric.copy()
если self.rho не None:
альфа += self.alpha_conductor
бета = 2 * pi * f * sqrt (ep_reff) / c
вернуть альфа + 1j*бета
@имущество
def Z0(self) -> npy.ndarray:
"""
Характеристическое сопротивление.
Примечание
----
Остерегайтесь путаницы с z0, импедансом порта среды. Возвращает
-------
Z0: :класс:`numpy.ndarray`
"""
вернуть self._z_characteristic
@имущество
def Z0_f(self) -> npy.ndarray:
"""
Псевдоним fos Характеристический импеданс для обратной совместимости.
Устарело, не используйте.
Примечание
----
Остерегайтесь путаницы с z0, импедансом порта среды.
Возвращает
-------
Z0: :класс:`numpy.ndarray`
"""
предупреждения.предупреждать(
"`Z0_f` устарел, используйте вместо него `Z0`",
Предупреждение об устаревании, уровень стека = 2
)
вернуть self._z_characteristic
Возвращает
-------
Z0: :класс:`numpy.ndarray`
"""
вернуть self._z_characteristic
@имущество
def Z0_f(self) -> npy.ndarray:
"""
Псевдоним fos Характеристический импеданс для обратной совместимости.
Устарело, не используйте.
Примечание
----
Остерегайтесь путаницы с z0, импедансом порта среды.
Возвращает
-------
Z0: :класс:`numpy.ndarray`
"""
предупреждения.предупреждать(
"`Z0_f` устарел, используйте вместо него `Z0`",
Предупреждение об устаревании, уровень стека = 2
)
вернуть self._z_characteristic
[документы] def analyse_dielectric(self, ep_r: NumberLike, tand: NumberLike,
f_low: NumberLike, f_high: NumberLike,
f_epr_tand: NumberLike, f: NumberLike,
номер: ул):
"""
Эта функция вычисляет относительную диэлектрическую проницаемость, зависящую от частоты. диэлектрических и тангенциальных потерь.
использованная литература
----------
.. [#] К. Свенссон, Г.Е. Дермер,
Моделирование межсоединений с потерями во временной области,
IEEE транс. по усовершенствованной упаковке, май 2001 г., N2, Vol. 24, стр. 191-196.
.. [#] Джорджевич, Р.М. Билич, В.Д. Ликар-Смилянич, Т.К. Саркар,
Широкополосная характеристика FR-4 в частотной области и во временной области
причинность,
IEEE транс. по ЭМС, вып. 43, №4, 2001, с. 662-667.
Возвращает
-------
ep_r_f::class:`numpy.ndarray`
tand_f::class:`numpy.ndarray`
"""
if diel == 'djordjevicsvensson':
# вычислить наклон для логарифмической шкалы частот, зависящий от tanD.
k = log((f_high + 1j * f_epr_tand) / (f_low + 1j * f_epr_tand))
fd = log((f_high + 1j * f) / (f_low + 1j * f))
ep_d = -tand * ep_r / imag(k)
# значение для частоты выше f_high
ep_inf = ep_r * (1.
диэлектрических и тангенциальных потерь.
использованная литература
----------
.. [#] К. Свенссон, Г.Е. Дермер,
Моделирование межсоединений с потерями во временной области,
IEEE транс. по усовершенствованной упаковке, май 2001 г., N2, Vol. 24, стр. 191-196.
.. [#] Джорджевич, Р.М. Билич, В.Д. Ликар-Смилянич, Т.К. Саркар,
Широкополосная характеристика FR-4 в частотной области и во временной области
причинность,
IEEE транс. по ЭМС, вып. 43, №4, 2001, с. 662-667.
Возвращает
-------
ep_r_f::class:`numpy.ndarray`
tand_f::class:`numpy.ndarray`
"""
if diel == 'djordjevicsvensson':
# вычислить наклон для логарифмической шкалы частот, зависящий от tanD.
k = log((f_high + 1j * f_epr_tand) / (f_low + 1j * f_epr_tand))
fd = log((f_high + 1j * f) / (f_low + 1j * f))
ep_d = -tand * ep_r / imag(k)
# значение для частоты выше f_high
ep_inf = ep_r * (1. + tand * real(k) / imag(k))
# вычислить комплексную диэлектрическую проницаемость
ep_r_f = ep_inf + ep_d * fd
# встать
tand_f = -imag(ep_r_f) / реальный(ep_r_f)
elif diel == 'частотный инвариант':
ep_r_f = ep_r - 1j * ep_r * tand
tand_f = tand
еще:
поднять ValueError('Неизвестная модель диэлектрической дисперсии')
вернуть ep_r_f, tand_f
+ tand * real(k) / imag(k))
# вычислить комплексную диэлектрическую проницаемость
ep_r_f = ep_inf + ep_d * fd
# встать
tand_f = -imag(ep_r_f) / реальный(ep_r_f)
elif diel == 'частотный инвариант':
ep_r_f = ep_r - 1j * ep_r * tand
tand_f = tand
еще:
поднять ValueError('Неизвестная модель диэлектрической дисперсии')
вернуть ep_r_f, tand_f
[документы] def analyse_quasi_static(self, ep_r: NumberLike,
w: NumberLike, h: NumberLike, t: NumberLike,
модель: стр):
"""
Эта функция вычисляет квазистатический импеданс микрополосковой
линия, значение эффективной диэлектрической проницаемости по фактору заполнения
и эффективная ширина из-за конечной толщины проводника для
заданные свойства микрополосковой линии и подложки.
использованная литература
----------
. . [#] Э. Хаммерстад и Ø. Дженсен,
Симпозиум «Точные модели для автоматизированного проектирования микрополосковых шин».
по теории и технике микроволнового излучения, стр. 407-409., июнь 1980 г.
.. [#] Х. А. Уиллер,
«Свойства линии передачи полосы на диэлектрическом листе на
Самолет, IEEE Trans. по теории и технике микроволнового излучения, т. 1, с. 25,
нет. 8, стр. 631-647, август 1977 г.
.. [#] М. В. Шнейдер,
"Микрополосковые линии для интегральных микросхем СВЧ",
Технический журнал Bell System, vol. 48, стр. 1421-1444, май 1969 г.
Возвращает
-------
zl_eff::class:`numpy.ndarray`
ep_reff::class:`numpy.ndarray`
"""
Z0 = кврт (mu_0 / эпсилон_0)
zl_eff = Z0
ep_reff = ep_r
w_эфф = ш
если модель == 'колесо':
# вычислить эффект толщины полосы
дв1 = 0
если t не None и t > 0:
dw1 = t / pi * log (4.
. [#] Э. Хаммерстад и Ø. Дженсен,
Симпозиум «Точные модели для автоматизированного проектирования микрополосковых шин».
по теории и технике микроволнового излучения, стр. 407-409., июнь 1980 г.
.. [#] Х. А. Уиллер,
«Свойства линии передачи полосы на диэлектрическом листе на
Самолет, IEEE Trans. по теории и технике микроволнового излучения, т. 1, с. 25,
нет. 8, стр. 631-647, август 1977 г.
.. [#] М. В. Шнейдер,
"Микрополосковые линии для интегральных микросхем СВЧ",
Технический журнал Bell System, vol. 48, стр. 1421-1444, май 1969 г.
Возвращает
-------
zl_eff::class:`numpy.ndarray`
ep_reff::class:`numpy.ndarray`
"""
Z0 = кврт (mu_0 / эпсилон_0)
zl_eff = Z0
ep_reff = ep_r
w_эфф = ш
если модель == 'колесо':
# вычислить эффект толщины полосы
дв1 = 0
если t не None и t > 0:
dw1 = t / pi * log (4. * exp (1.) / sqrt ((t / h) ** 2) + \
(1. / pi / (вес / т + 1,1))**2)
dwr = (1. + 1. / ep_r) / 2. * dw1
вр = ш + двр
w_eff = wr
# вычислить волновое сопротивление
если (ш/ч) < 3,3:
cp = log(4. * h/wr + sqrt((4 * h/wr)**2 + 2))
b = (ep_r - 1.) / (ep_r + 1.) / \
2 * (лог(pi/2.) + log(4./pi)/ep_r)
zl_eff = (cp - b) * Z0 / pi / sqrt (2 * (ep_r + 1.))
еще:
cp = 1 + log(pi/2.) + log(wr/h/2. + 0,94)
d = 1. / pi / 2. * (1. + log(pi ** 2 / 16.)) * (ep_r - 1.) \
/ ep_r**2
x = 2. * log(2.) / pi + wr / h / 2. + (ep_r + 1.) / 2 / pi / \
ep_r * cp + d
zl_eff = Z0 / 2 / x / sqrt (ep_r)
# вычислить эффективную диэлектрическую проницаемость
если (ш/ч) < 1,3:
а = log(8 * ч/ч) + (ч/ч)**2/32
b = (ep_r - 1.
* exp (1.) / sqrt ((t / h) ** 2) + \
(1. / pi / (вес / т + 1,1))**2)
dwr = (1. + 1. / ep_r) / 2. * dw1
вр = ш + двр
w_eff = wr
# вычислить волновое сопротивление
если (ш/ч) < 3,3:
cp = log(4. * h/wr + sqrt((4 * h/wr)**2 + 2))
b = (ep_r - 1.) / (ep_r + 1.) / \
2 * (лог(pi/2.) + log(4./pi)/ep_r)
zl_eff = (cp - b) * Z0 / pi / sqrt (2 * (ep_r + 1.))
еще:
cp = 1 + log(pi/2.) + log(wr/h/2. + 0,94)
d = 1. / pi / 2. * (1. + log(pi ** 2 / 16.)) * (ep_r - 1.) \
/ ep_r**2
x = 2. * log(2.) / pi + wr / h / 2. + (ep_r + 1.) / 2 / pi / \
ep_r * cp + d
zl_eff = Z0 / 2 / x / sqrt (ep_r)
# вычислить эффективную диэлектрическую проницаемость
если (ш/ч) < 1,3:
а = log(8 * ч/ч) + (ч/ч)**2/32
b = (ep_r - 1. ) / (ep_r + 1.) / \
2 * (лог(pi/2.) + log(4./pi)/ep_r)
ep_reff = (ep_r + 1.) / 2. * (a / (a - b))**2
еще:
# qucsator 4.0137, но doc 0.94 * 2 = 1,88
d = (ep_r - 1.)/2./pi/ep_r*\
(log(2,1349 * wr/h + 4,0137) - 0,5169/ep_r)
e = wr / h / 2 + 1. / pi * log (8,5397 * wr / h + 16,0547)
ep_reff = ep_r * ((e - d) / e)**2
Элиф модель == 'Шнайдер':
и = ш / ч
дв = 0
# рассмотрим уравнения толщины полосы
если t не None и t > 0:
если t < (w/2):
если и < (1./пи/2):
аргумент = 2 * пи * вес / т
еще:
аргумент = ч / т
dw = t/pi * (1. + log(2 * arg))
если (t/dw) >= 0,75:
дв = 0
w_eff = w + dw
u = w_эфф/ч
# эффективная диэлектрическая проницаемость
ep_reff = (ep_r + 1.
) / (ep_r + 1.) / \
2 * (лог(pi/2.) + log(4./pi)/ep_r)
ep_reff = (ep_r + 1.) / 2. * (a / (a - b))**2
еще:
# qucsator 4.0137, но doc 0.94 * 2 = 1,88
d = (ep_r - 1.)/2./pi/ep_r*\
(log(2,1349 * wr/h + 4,0137) - 0,5169/ep_r)
e = wr / h / 2 + 1. / pi * log (8,5397 * wr / h + 16,0547)
ep_reff = ep_r * ((e - d) / e)**2
Элиф модель == 'Шнайдер':
и = ш / ч
дв = 0
# рассмотрим уравнения толщины полосы
если t не None и t > 0:
если t < (w/2):
если и < (1./пи/2):
аргумент = 2 * пи * вес / т
еще:
аргумент = ч / т
dw = t/pi * (1. + log(2 * arg))
если (t/dw) >= 0,75:
дв = 0
w_eff = w + dw
u = w_эфф/ч
# эффективная диэлектрическая проницаемость
ep_reff = (ep_r + 1. ) / 2. + (ep_r - 1.) / 2. / sqrt (1. + 10. / u)
# волновое сопротивление
если и < 1.:
z = 1./pi/2.*log(8./u + u/4)
еще:
z = 1. / (u + 2,42 - 0,44 / u + (1. - 1. / u)**6)
zl_eff = Z0 * z / sqrt (ep_reff)
Элиф модель == 'hammerstadjensen':
и = ш / ч
если t не None:
т = т/ч
ду1 = 0.
# вычислить эффект толщины полосы
если t не None и t > 0:
# Формула Qucs 11.22 неверна, вместо нее необходимо использовать нормализованную w (см. статью Hammerstad and Jensen)
# Нормализованный w называется u и фактически используется в исходном коде qucsator
# coth(альфа) = 1/tanh(альфа)
du1 = t / pi * log(1. + 4. * exp(1.) / t * tanh(sqrt(6.517 * u))**2)
# sech(альфа) = 1/cosh(альфа)
dur = du1 * (1. + 1. / ch(sqrt(ep_r - 1.
) / 2. + (ep_r - 1.) / 2. / sqrt (1. + 10. / u)
# волновое сопротивление
если и < 1.:
z = 1./pi/2.*log(8./u + u/4)
еще:
z = 1. / (u + 2,42 - 0,44 / u + (1. - 1. / u)**6)
zl_eff = Z0 * z / sqrt (ep_reff)
Элиф модель == 'hammerstadjensen':
и = ш / ч
если t не None:
т = т/ч
ду1 = 0.
# вычислить эффект толщины полосы
если t не None и t > 0:
# Формула Qucs 11.22 неверна, вместо нее необходимо использовать нормализованную w (см. статью Hammerstad and Jensen)
# Нормализованный w называется u и фактически используется в исходном коде qucsator
# coth(альфа) = 1/tanh(альфа)
du1 = t / pi * log(1. + 4. * exp(1.) / t * tanh(sqrt(6.517 * u))**2)
# sech(альфа) = 1/cosh(альфа)
dur = du1 * (1. + 1. / ch(sqrt(ep_r - 1. ))) / 2.
и1 = и + du1
ур = и + продолжительность
w_eff = ур * ч
# вычислить импеданс для однородной среды
zr = хаммерстад_zl (ур)
z1 = хаммерстад_zl(u1)
# вычислить эффективную диэлектрическую проницаемость
a, b = Hammerstad_ab(ur, ep_r)
e = Hammerstad_er (ur, ep_r, a, b)
# вычислить окончательный характеристический импеданс и диэлектрическую проницаемость
# включая эффекты толщины полосы
zl_eff = zr / sqrt(e)
ep_reff = e * (z1 / zr)**2
еще:
поднять ValueError('Неизвестная квазистатическая модель микрополосковой линии')
вернуть zl_eff, ep_reff, w_eff
))) / 2.
и1 = и + du1
ур = и + продолжительность
w_eff = ур * ч
# вычислить импеданс для однородной среды
zr = хаммерстад_zl (ур)
z1 = хаммерстад_zl(u1)
# вычислить эффективную диэлектрическую проницаемость
a, b = Hammerstad_ab(ur, ep_r)
e = Hammerstad_er (ur, ep_r, a, b)
# вычислить окончательный характеристический импеданс и диэлектрическую проницаемость
# включая эффекты толщины полосы
zl_eff = zr / sqrt(e)
ep_reff = e * (z1 / zr)**2
еще:
поднять ValueError('Неизвестная квазистатическая модель микрополосковой линии')
вернуть zl_eff, ep_reff, w_eff
[документы] def analyse_diversion(self, zl_eff: NumberLike, ep_reff: NumberLike,
ep_r: NumberLike, wr: NumberLike, w_eff: NumberLike,
h: NumberLike, t: NumberLike, f: NumberLike,
дисп: ул):
"""
Эта функция вычисляет частотно-зависимую характеристику
учет импеданса и эффективной диэлектрической проницаемости для микрополосковой линии
частотная дисперсия. использованная литература
----------
.. [#] М. Кобаяши,
«Формула дисперсии, отвечающая последним требованиям к микрополосковым технологиям».
CAD", IEEE Trans. on Microwave Theory and Techniques, vol. 36,
нет. 8, стр. 1246-1250, 19 августа.88.
.. [#] М. В. Шнайдер, "Микрополосковая дисперсия", Труды
IEEE, письма, том. 60, январь 1972 г., стр. 144–146.
.. [#] М. Киршнинг и Р. Х. Янсен,
«Точная модель эффективной диэлектрической проницаемости микрополоскового
с достоверностью до частот миллиметрового диапазона", Электроника
Письма, том. 8, нет. 6, стр. 272-273, март 1982 г.
.. [#] Р. Х. Янсен и М. Киршнинг,
«Аргументы и точная модель силовой токовой формулировки
Характеристическое сопротивление микрополосковой полосы",
Archiv für Elektronik und Übertragungstechnik (AEÜ), vol. 37,
стр. 108-112, 1983.
использованная литература
----------
.. [#] М. Кобаяши,
«Формула дисперсии, отвечающая последним требованиям к микрополосковым технологиям».
CAD", IEEE Trans. on Microwave Theory and Techniques, vol. 36,
нет. 8, стр. 1246-1250, 19 августа.88.
.. [#] М. В. Шнайдер, "Микрополосковая дисперсия", Труды
IEEE, письма, том. 60, январь 1972 г., стр. 144–146.
.. [#] М. Киршнинг и Р. Х. Янсен,
«Точная модель эффективной диэлектрической проницаемости микрополоскового
с достоверностью до частот миллиметрового диапазона", Электроника
Письма, том. 8, нет. 6, стр. 272-273, март 1982 г.
.. [#] Р. Х. Янсен и М. Киршнинг,
«Аргументы и точная модель силовой токовой формулировки
Характеристическое сопротивление микрополосковой полосы",
Archiv für Elektronik und Übertragungstechnik (AEÜ), vol. 37,
стр. 108-112, 1983. .. [#] Э. Ямасита, К. Ацуки и Т. Уэда,
"Примерная дисперсионная формула микрополосковых линий для
Компьютерное проектирование интегральных схем СВЧ",
IEEE транс. по теории и технике микроволнового излучения, т. 1, с. 27,
стр. 1036-1038, декабрь 1979 г.
Возвращает
-------
z::class:`numpy.ndarray`
e::class:`numpy.ndarray`
"""
u = Вт/ч
если дисп == 'Шнайдер':
k = sqrt (ep_reff / ep_r)
fn = 4. * h * f / c * sqrt (ep_r - 1.)
фн2 = фн**2
e = ep_ref * ((1. + fn2) / (1. + k * fn2))**2
z = zl_eff * sqrt (ep_reff / e)
elif disp == 'hammerstadjensen':
Z0 = кврт (mu_0 / эпсилон_0)
g = pi**2 / 12 * (ep_r - 1) / ep_reff * sqrt (2 * pi * zl_eff / Z0)
fp = (2 * mu_0 * h * f) / zl_eff
e = ep_r - (ep_r - ep_reff) / (1 + g * fp**2)
z = zl_eff * sqrt (ep_reff / e) * (e - 1) / (ep_reff - 1)
Элиф дисп == 'киршнингянсен':
фн = ф * ч * 1е-6
e = kirsching_er (u, fn, ep_r, ep_reff)
z, _ = kirsching_zl(u, fn, ep_r, ep_reff, e, zl_eff)
Элиф дисп == 'ямасита':
k = sqrt (ep_r / ep_reff)
fp = 4 * h * f / c * sqrt (ep_r - 1) * \
(0,5 + (1 + 2 * log10(1 + u))**2)
e = ep_reff * ((1 + k * fp**1,5/4) / (1 + fp**1,5/4))**2
# qucs сохраняет здесь квазистатический импеданс
если self.
.. [#] Э. Ямасита, К. Ацуки и Т. Уэда,
"Примерная дисперсионная формула микрополосковых линий для
Компьютерное проектирование интегральных схем СВЧ",
IEEE транс. по теории и технике микроволнового излучения, т. 1, с. 27,
стр. 1036-1038, декабрь 1979 г.
Возвращает
-------
z::class:`numpy.ndarray`
e::class:`numpy.ndarray`
"""
u = Вт/ч
если дисп == 'Шнайдер':
k = sqrt (ep_reff / ep_r)
fn = 4. * h * f / c * sqrt (ep_r - 1.)
фн2 = фн**2
e = ep_ref * ((1. + fn2) / (1. + k * fn2))**2
z = zl_eff * sqrt (ep_reff / e)
elif disp == 'hammerstadjensen':
Z0 = кврт (mu_0 / эпсилон_0)
g = pi**2 / 12 * (ep_r - 1) / ep_reff * sqrt (2 * pi * zl_eff / Z0)
fp = (2 * mu_0 * h * f) / zl_eff
e = ep_r - (ep_r - ep_reff) / (1 + g * fp**2)
z = zl_eff * sqrt (ep_reff / e) * (e - 1) / (ep_reff - 1)
Элиф дисп == 'киршнингянсен':
фн = ф * ч * 1е-6
e = kirsching_er (u, fn, ep_r, ep_reff)
z, _ = kirsching_zl(u, fn, ep_r, ep_reff, e, zl_eff)
Элиф дисп == 'ямасита':
k = sqrt (ep_r / ep_reff)
fp = 4 * h * f / c * sqrt (ep_r - 1) * \
(0,5 + (1 + 2 * log10(1 + u))**2)
e = ep_reff * ((1 + k * fp**1,5/4) / (1 + fp**1,5/4))**2
# qucs сохраняет здесь квазистатический импеданс
если self. compatibility_mode == 'qucs':
z = npy.ones (f.shape) * zl_eff
# по умолчанию использовать Kirschning Jansen для дисперсии импеданса
еще:
фн = ф * ч * 1е-6
z, _ = kirsching_zl(wr/h, fn, ep_r, ep_reff, e, zl_eff)
Элиф дисп == 'кобаяши':
fk = c * arctan(ep_r * sqrt((ep_reff - 1) / (ep_r - ep_reff)))/ \
(2 * pi * h * sqrt (ep_r - ep_reff))
fh = fk / (0,75 + (0,75 - 0,332 / (ep_r**1,73)) * u)
нет = 1 + 1 / (1 + sqrt(u)) + 0,32 * (1 / (1 + sqrt(u))**3
nc = npy.where(u < 0,7,
1 + 1,4 / (1 + u) * (0,15 - 0,235 * exp (-0,45 * f / fh)),
1)
n = npy.where (нет * nc < 2,32, нет * nc, 2,32)
e = ep_r - (ep_r - ep_reff) / (1 + (f / fh)**n)
# qucs сохраняет здесь квазистатический импеданс
если self.compatibility_mode == 'qucs':
z = npy.ones (f.shape) * zl_eff
# по умолчанию использовать Kirschning Jansen для дисперсии импеданса
еще:
фн = ф * ч * 1е-6
z, _ = kirsching_zl(wr/h, fn, ep_r, ep_reff, e, zl_eff)
Элиф дисп == 'нет':
e = единицы (f.
compatibility_mode == 'qucs':
z = npy.ones (f.shape) * zl_eff
# по умолчанию использовать Kirschning Jansen для дисперсии импеданса
еще:
фн = ф * ч * 1е-6
z, _ = kirsching_zl(wr/h, fn, ep_r, ep_reff, e, zl_eff)
Элиф дисп == 'кобаяши':
fk = c * arctan(ep_r * sqrt((ep_reff - 1) / (ep_r - ep_reff)))/ \
(2 * pi * h * sqrt (ep_r - ep_reff))
fh = fk / (0,75 + (0,75 - 0,332 / (ep_r**1,73)) * u)
нет = 1 + 1 / (1 + sqrt(u)) + 0,32 * (1 / (1 + sqrt(u))**3
nc = npy.where(u < 0,7,
1 + 1,4 / (1 + u) * (0,15 - 0,235 * exp (-0,45 * f / fh)),
1)
n = npy.where (нет * nc < 2,32, нет * nc, 2,32)
e = ep_r - (ep_r - ep_reff) / (1 + (f / fh)**n)
# qucs сохраняет здесь квазистатический импеданс
если self.compatibility_mode == 'qucs':
z = npy.ones (f.shape) * zl_eff
# по умолчанию использовать Kirschning Jansen для дисперсии импеданса
еще:
фн = ф * ч * 1е-6
z, _ = kirsching_zl(wr/h, fn, ep_r, ep_reff, e, zl_eff)
Элиф дисп == 'нет':
e = единицы (f. shape) * ep_reff
z = единицы (f.shape) * zl_eff
еще:
поднять ValueError('Неизвестная модель микрополосковой дисперсии')
вернуть г, е
shape) * ep_reff
z = единицы (f.shape) * zl_eff
еще:
поднять ValueError('Неизвестная модель микрополосковой дисперсии')
вернуть г, е
[документы] def analyse_loss(self, ep_r: NumberLike, ep_reff: NumberLike,
tand: NumberLike, rho: NumberLike, mu_r: NumberLike,
zl_eff_f1: NumberLike, zl_eff_f2: NumberLike,
f: NumberLike, w: NumberLike, t: NumberLike,
D: Число лайков):
"""
Функция рассчитывает потери в проводнике и диэлектрике
одиночная микрополосковая линия с использованием правила приращения индуктивности Уилера.
использованная литература
----------
.. [#] H.A. Wheeler, «Формулы скин-эффекта»,
Труды IRE, vol. 30, нет. 9, стр. 412-424, сентябрь 1942 г.
Возвращает
-------
a_conductor::class:`numpy.ndarray`
a_dielectric::class:`numpy. ndarray`
"""
# ограничено только моделями Hammerstad и Jensen
Z0 = npy.sqrt (mu_0/epsilon_0)
# потери в проводнике
если t не None и t > 0:
если ро равно None:
поднять(AttributeError('должно быть указано удельное сопротивление rho. '
'см. справку по инициализатору'))
еще:
Rs = поверхностное_сопротивление (f = f, rho = rho, mu_r = 1)
ds = глубина кожи (f, rho, mu_r)
если (npy.any (t < 3 * ds)):
предупреждения.предупреждать(
«Расчет потерь в проводнике недействителен для линии»
'высота t ({}) < 3 * глубина кожи ({})'.format(t, ds[0]),
Предупреждение во время выполнения
)
# текущий коэффициент распределения
Ki = exp(-1,2 * ((zl_eff_f1 + zl_eff_f2) / 2 / Z0)**0,7)
# D – среднеквадратическая шероховатость поверхности.
ndarray`
"""
# ограничено только моделями Hammerstad и Jensen
Z0 = npy.sqrt (mu_0/epsilon_0)
# потери в проводнике
если t не None и t > 0:
если ро равно None:
поднять(AttributeError('должно быть указано удельное сопротивление rho. '
'см. справку по инициализатору'))
еще:
Rs = поверхностное_сопротивление (f = f, rho = rho, mu_r = 1)
ds = глубина кожи (f, rho, mu_r)
если (npy.any (t < 3 * ds)):
предупреждения.предупреждать(
«Расчет потерь в проводнике недействителен для линии»
'высота t ({}) < 3 * глубина кожи ({})'.format(t, ds[0]),
Предупреждение во время выполнения
)
# текущий коэффициент распределения
Ki = exp(-1,2 * ((zl_eff_f1 + zl_eff_f2) / 2 / Z0)**0,7)
# D – среднеквадратическая шероховатость поверхности. Kr = 1 + 2 / pi * arctan (1,4 * (D/ds)**2)
a_проводник = Rs / (zl_eff_f1 * w) * Ki * Kr
еще:
a_conductor = нули (f.shape)
# диэлектрические потери
l0 = с/f
a_dielectric = pi * ep_r / (ep_r - 1) * (ep_reff - 1) / \
sqrt(ep_reff) * tand / l0
вернуть a_conductor, a_dielectric
Kr = 1 + 2 / pi * arctan (1,4 * (D/ds)**2)
a_проводник = Rs / (zl_eff_f1 * w) * Ki * Kr
еще:
a_conductor = нули (f.shape)
# диэлектрические потери
l0 = с/f
a_dielectric = pi * ep_r / (ep_r - 1) * (ep_reff - 1) / \
sqrt(ep_reff) * tand / l0
вернуть a_conductor, a_dielectric
def Hammerstad_ab(u: NumberLike, ep_r: NumberLike) -> NumberLike:
"""
Параметры Хаммерстада для дисперсии относительной диэлектрической проницаемости.
"""
a = 1. + log((u**4 + (u / 52.)**2) / (u**4 + 0,432)) / 49. \
+ log(1 + (u/18,1)**3)/18,7
b = 0,564 * ((ep_r - 0,9) / (ep_r + 3.))**0,053
вернуть а, б
def Hammerstad_zl(u: NumberLike) -> NumberLike:
"""
Квазистатический импеданс Хаммерстада.
"""
фу = 6 + (2 * пи - 6) * ехр (- (30,666 / u) ** 0,7528)
Z0 = квадрат (mu_0/epsilon_0)
вернуть Z0 / 2. / pi * log (fu / u + sqrt (1. + (2. / u) ** 2))
def Hammerstad_er(u: NumberLike, ep_r: NumberLike, a: NumberLike,
b: NumberLike) -> NumberLike:
"""
Квазистатическая относительная диэлектрическая проницаемость Хаммерстада. """
return (ep_r + 1) / 2 + (ep_r - 1) / 2 * (1. + 10. / u)**(-a * b)
def kirsching_zl(u: NumberLike, fn: NumberLike,
ep_r: NumberLike, ep_reff: NumberLike, ep_reff_f: NumberLike,
zl_eff: число лайков):
"""
Дисперсия импеданса Киршнинг-Янсена.
"""
#fn = f * h * 1e-6 # ГГц-мм
R1 = npy.минимум (0,03891 * воз_р**1,4, 20.)
R2 = npy.минимум (0,2671 * u**7, 20.)
R3 = 4,766 * ехр (-3,228 * u**0,641)
R4 = 0,016 + (0,0514 * ep_r)**4,524
R5 = (фн / 28,843)**12
R6 = npy.минимум (22,20 * u ** 1,92, 20.)
R7 = 1,206 - 0,3144 * exp(-R1) * (1 - exp(-R2))
R8 = 1 + 1,275 * (1 - exp(-0,004625 * R3 * ep_r**1,674 \
* (фн / 18,365)**2,745))
R9 = 5,086 * R4 * R5/(0,3838 + 0,386 * R4) \
* ехр(-R6) / (1 + 1,2992 * R5) \
* (ep_r - 1)**6 / (1 + 10 * (ep_r - 1)**6)
R10 = 0,00044 * ep_r** 2,136 + 0,0184
Р11 = (лн/190,47)**6 / (1 + 0,0962 * (фн / 19,47)**6)
R12 = 1 / (1 + 0,00245 * u**2)
R13 = 0,9408 * ep_reff_f**R8 - 0,9603
R14 = (0,9408 - R9) * ep_reff**R8 - 0,9603
R15 = 0,707 * R10 * (фн / 12,3)**1,097
R16 = 1 + 0,0503 * ep_r**2 * R11 * (1 - exp(-(u / 15)**6))
R17 = R7 * (1 - 1,1241 * R12 / R16 \
*exp(-0,026 * fn**1,15656 - R15))
возврат zl_eff * (R13/R14)**R17, R17
def kirsching_er(u: NumberLike, fn: NumberLike,
ep_r: NumberLike, ep_reff: NumberLike):
"""
Дисперсия относительной диэлектрической проницаемости Киршнинг-Янсена.
"""
return (ep_r + 1) / 2 + (ep_r - 1) / 2 * (1. + 10. / u)**(-a * b)
def kirsching_zl(u: NumberLike, fn: NumberLike,
ep_r: NumberLike, ep_reff: NumberLike, ep_reff_f: NumberLike,
zl_eff: число лайков):
"""
Дисперсия импеданса Киршнинг-Янсена.
"""
#fn = f * h * 1e-6 # ГГц-мм
R1 = npy.минимум (0,03891 * воз_р**1,4, 20.)
R2 = npy.минимум (0,2671 * u**7, 20.)
R3 = 4,766 * ехр (-3,228 * u**0,641)
R4 = 0,016 + (0,0514 * ep_r)**4,524
R5 = (фн / 28,843)**12
R6 = npy.минимум (22,20 * u ** 1,92, 20.)
R7 = 1,206 - 0,3144 * exp(-R1) * (1 - exp(-R2))
R8 = 1 + 1,275 * (1 - exp(-0,004625 * R3 * ep_r**1,674 \
* (фн / 18,365)**2,745))
R9 = 5,086 * R4 * R5/(0,3838 + 0,386 * R4) \
* ехр(-R6) / (1 + 1,2992 * R5) \
* (ep_r - 1)**6 / (1 + 10 * (ep_r - 1)**6)
R10 = 0,00044 * ep_r** 2,136 + 0,0184
Р11 = (лн/190,47)**6 / (1 + 0,0962 * (фн / 19,47)**6)
R12 = 1 / (1 + 0,00245 * u**2)
R13 = 0,9408 * ep_reff_f**R8 - 0,9603
R14 = (0,9408 - R9) * ep_reff**R8 - 0,9603
R15 = 0,707 * R10 * (фн / 12,3)**1,097
R16 = 1 + 0,0503 * ep_r**2 * R11 * (1 - exp(-(u / 15)**6))
R17 = R7 * (1 - 1,1241 * R12 / R16 \
*exp(-0,026 * fn**1,15656 - R15))
возврат zl_eff * (R13/R14)**R17, R17
def kirsching_er(u: NumberLike, fn: NumberLike,
ep_r: NumberLike, ep_reff: NumberLike):
"""
Дисперсия относительной диэлектрической проницаемости Киршнинг-Янсена. """
# в документе fn выражена в ГГц-см, а в Qucs - ГГц-мм, таким образом, коэффициент
# 10 для всех констант, которые умножают или делят fn
P1 = 0,27488 + (0,6315 + 0,525 / ( 1+ 0,0157 * fn)**20) * u \
-0,065683 * ехр (-8,7513 * и)
P2 = 0,33622 * (1 -exp(-0,03442 * ep_r))
P3 = 0,0363 * exp (-4,6 * u) * (1 - exp (- (fn / 38,7) ** 4,97))
P4 = 1 + 2,751 * (1 - exp(-(ep_r / 15,916)**8))
Pf = P1 * P2 * ((0,1844 + P3 * P4) * fn)**1,5763
вернуть ep_r - (ep_r - ep_reff) / (1 + Pf)
"""
# в документе fn выражена в ГГц-см, а в Qucs - ГГц-мм, таким образом, коэффициент
# 10 для всех констант, которые умножают или делят fn
P1 = 0,27488 + (0,6315 + 0,525 / ( 1+ 0,0157 * fn)**20) * u \
-0,065683 * ехр (-8,7513 * и)
P2 = 0,33622 * (1 -exp(-0,03442 * ep_r))
P3 = 0,0363 * exp (-4,6 * u) * (1 - exp (- (fn / 38,7) ** 4,97))
P4 = 1 + 2,751 * (1 - exp(-(ep_r / 15,916)**8))
Pf = P1 * P2 * ((0,1844 + P3 * P4) * fn)**1,5763
вернуть ep_r - (ep_r - ep_reff) / (1 + Pf)
skrf.media.cpw — scikit-rf Документация
""" cpw (:mod:`skrf.media.cpw`) ======================================== .. автосуммирование:: :toctree: сгенерировано/ CPW """ из numpy import sqrt, log, zeros, any, tanh, sinh, exp, real, imag из scipy.constants импортировать epsilon_0, mu_0, c, pi из scipy.special импорт эллипс из .media импорт Медиа из ..tlineFunctions импортировать surface_resistivity, skin_depth из ..констант импортировать NumberLike набрав import Union, TYPE_CHECKING предупреждения об импорте если TYPE_CHECKING: из .. частота импорт Частота
[документы]класс CPW(Медиа): р""" Компланарный волновод. Компланарная волноводная линия передачи определяется шириной, расстояние и толщина на данной подложке с относительной диэлектрической проницаемостью определенная высота. Линия имеет удельное сопротивление проводника и тангенциальные потери фактор. Тыльная сторона полосы может быть выполнена из воздуха или металла (заземленная). компланарный волновод). Этот класс основан на технической документации [QUCSa]_ и исходники, предоставленные проектом qucs [QUCSb]_. Кроме того, Джорджевич [DBLS01]_ /Svensson [SvDe01]_ широкополосный диэлектрик Дебая Считается, что модель обеспечивает более реалистичное моделирование широкополосного доступа. микрополосковая с причинно-следственным откликом во временной области. Предусмотрен режим совместимости, имитирующий поведение QUCS или ADS компании Keysight. Существуют известные различия в выходе этих тренажеры.
Квазистатические модели волнового сопротивления и эффективного диэлектрическая проницаемость дает значение при нулевой частоте. Дисперсионные модели вычислить частотно-зависимые значения этих переменных. * Модель квазистатического волнового сопротивления и эффективной диэлектрической проницаемости используйте [GhNa84]_ и [GhNa83]_. Модели скорректированы с учетом толщины полосы с использованием подхода первого порядка, описанного в [GGBB96]_. Сравнение показывает, что симулятор ADS использует другую коррекцию толщины. метод, соответствующий документу ADS, основанному на [Cohn60]_. Этот второй метод не реализован в skrf. * Использование модели частотной дисперсии импеданса и эффективной диэлектрической проницаемости [FGVM91]_ и [GMDK97]_. * Модель потерь рассчитана с использованием правила приращения индуктивности Уилера. [Whee42]_ применяется к копланарному волноводу [OwWu58]_ и [Ghio93]_. Параметры ---------- частота : :class:`~skrf.
frequency.Frequency` объект, необязательный полоса частот носителя. По умолчанию нет. z0 : число, массив или None (по умолчанию None) импеданс порта для среды. Требуется только в том случае, если отличается от волновое сопротивление Z0 линии передачи. в омах w : число или массив ширина центральной жилы, м. По умолчанию 3e-3 м. s : число или массив шаг (ширина зазора), м. По умолчанию 0,3e-3 м. h : число или массив высота подложки между тыльной стороной и проводником, м. По умолчанию 1,55 м (эквивалентно бесконечной высоте для w и s по умолчанию). t : число или массив, необязательный толщина проводника, м. По умолчанию — None (без коррекции ширины). для учета толщины полосы). has_metal_backside : bool, по умолчанию False Если обратная сторона воздушная (ложь) или металлическая (правда) ep_r : число или массив, необязательный относительная диэлектрическая проницаемость подложки на частоте f_epr_tand, нет единицы.
По умолчанию 4,5. номер : ул. модель дисперсии диэлектрической частоты в: * 'джорджевичсвенссон' (по умолчанию) * 'частотно-инвариантный' rho : число, или массив, или None Удельное сопротивление проводника, Ом/м. По умолчанию 1,68e-8 Ом/м (медь). tand : число или массив коэффициент диэлектрических потерь на частоте f_epr_tand. По умолчанию 0. f_low : число или массив более низкая частота для широкополосного диэлектрика Дебая Джорджевича/Свенсона модель, в Гц. По умолчанию 1 кГц. f_high : число или массив более высокая частота для широкополосного диэлектрика Дебая Джорджевича / Свенссона модель, в Гц. По умолчанию 1 ТГц. f_epr_tand : число или массив частота измерения ep_r и tand диэлектрика, Гц. По умолчанию 1 ГГц. compatibility_mode: str или None (по умолчанию) Если установлено значение «qucs», происходит следующее поведение: * Волновое сопротивление будет действительным (без мнимой части из-за tand) \*args, \*\*kwargs : аргументы, аргументы ключевого слова передается в конструктор :class:`~skrf.
media.media.Media` (:func:`~skrf.media.media.Media.__init__` Примечание ---- При толщине полосы менее 3 толщин скин-слоя потери модель дает чрезмерно оптимистичные результаты, и средства массовой информации вынесут предупреждение. При постоянном токе потери в линии могут быть меньше, чем в ее проводнике. сопротивление, которое не является физическим. использованная литература ---------- .. [QUCSa] http://qucs.sourceforge.net/docs/technical.pdf .. [QUCSb] http://www.qucs.sourceforge.net/ .. [DBLS01] Джорджевич, Р.М. Билич, В.Д. Ликар-Смилянич, Т.К. Саркар, Широкополосная характеристика FR-4 в частотной области и во временной области причинность, IEEE транс. по ЭМС, вып. 43, №4, 2001, с. 662-667. .. [SvDe01] К. Свенссон, Г.Е. Дермер, Моделирование межсоединений с потерями во временной области, IEEE транс. по усовершенствованной упаковке, май 2001 г., N2, Vol. 24, стр. 191-196.
.. [GhNa84] Г. Гионе и К. Налди. "Аналитические формулы для копланарных прямых в гибридных и монолитных МИС», Electronics Letters, Том. 20, № 4, 16 февраля 1984 г., стр. 179-181. .. [GhNa83] Г. Гионе и К. Налди. "Параметры копланарных волноводов с Нижние общие плоскости», Electronics Letters, Том. 19, № 18, 1 сентября 1983 г., стр. 734-735. .. [Cohn60] SB Cohn, "Поправки на толщину для емкостных препятствий и Ленточные проводники», IRE Trans. on Microwave Theory and Techniques, Том. МТТ-8, 19 ноября60, стр. 638-644. .. [GGBB96] KC Gupta, R. Garg, IJ Bahl, and P. Bhartia, Microstrip Линии и игровые линии, 2-е изд. Artech House, Inc., 1996. .. [FGVM91] М. Ю. Франкель, С. Гупта, Дж. А. Вальдманис и Г. А. Муру, "Терагерцовые характеристики затухания и дисперсии компланарных Линии передачи» IEEE Trans. on Microwave Theory and Techniques, об. 39, нет. 6, стр. 910-916, июнь 1991 г. .. [GMDK97] С. Геворгян, Т.
Мартинссон, А. Деленив, Э. Коллберг и И. Вендик, "Простое и точное дисперсионное выражение для эффективная диэлектрическая проницаемость копланарных волноводов» в Труды микроволн, антенн и распространения, об. 144, нет. 2. IEE, 19 апреля.97, стр. 145-148. .. [Whee42] H.A. Wheeler, "Формулы скин-эффекта", Труды IRE, vol. 30, нет. 9, стр. 412-424, сентябрь 1942 г. .. [OwWu58] Г. Х. Оуян и Т. Т. Ву, "Приблизительные параметры слота Линии и их дополнение" Операции IRE по антеннам и Распространение, стр. 49-55, январь 1958 г. .. [Ghio93] G. Ghione, "Аналитическая модель потерь Общие асимметричные копланарные линии в гибридных и монолитных МИС» IEEE транс. по теории и технике микроволнового излучения, об. 41, нет. 9, стр. 1499-1510, сентябрь 1993 г. """
[документы] def __init__(self, Frequency: Union['Frequency', None] = None, z0: Union[NumberLike, None] = Нет, w: NumberLike = 3e-3, s: NumberLike = 0,3e-3, ч: число лайков = 1,55, ep_r: NumberLike = 4,5, t: Union[NumberLike, None] = None, diel: str = 'djordjevicsvensson', ро: Union[NumberLike, None] = 1.
68e-8, tand: NumberLike = 0, f_low: NumberLike = 1e3, f_high: NumberLike = 1e12, f_epr_tand: NumberLike = 1e9, has_metal_backside: логическое значение = ложь, compatibility_mode: Union[str, None] = None, *args, **kwargs): Media.__init__(я, частота=частота,z0=z0) self.w, self.s, self.h, self.t, self.ep_r, self.tand, self.rho =\ w, s, h, t, ep_r, tand, rho селф.диэль = дил self.f_low, self.f_high, self.f_epr_tand = f_low, f_high, f_epr_tand self.has_metal_backside = has_metal_backside self.compatibility_mode = режим_совместимости # изменение эффективной диэлектрической проницаемости в зависимости от частоты # Не реализовано в QUCS, но реализовано в ADS. # 'частотный инвариант' даст постоянное комплексное значение с реальным # часть, совместимая с qucs, и мнимая часть из-за tand self.ep_r_f, self.
tand_f = self.analyse_dielectric( self.ep_r, self.tand, self.f_low, self.f_high, self.f_epr_tand, self.frequency.f, селф.диэль) # квазистатическая эффективная диэлектрическая проницаемость подложки + линии и # полное сопротивление копланарного волновода # qucs использует ep_r с действительным знаком, что дает импеданс с действительным знаком если compatibility_mode == 'qucs': self.zl_eff, self.ep_reff, k1, kk1, kpk1 = \ self.analyse_quasi_static( реальный (self.ep_r_f), w, s, h, t, has_metal_backside) еще: self.zl_eff, self.ep_reff, k1, kk1, kpk1 = \ self.analyse_quasi_static( self.ep_r_f, w, s, h, t, has_metal_backside) # анализировать дисперсию импеданса и относительной диэлектрической проницаемости если compatibility_mode == 'qucs': self._z_characteristic, self.ep_reff_f = self.
analyse_дисперсия( self.zl_eff, self.ep_reff, реальный (self.ep_r_f), w, s, h, собственная.частота.f) # в объявлениях не используется частотная дисперсия для cpw/cpwg (так грустно) elif compatibility_mode == 'объявления': self._z_characteristic = self.zl_eff self.ep_reff_f = self.ep_reff # по умолчанию использовать частотную дисперсию и комплексную диэлектрическую проницаемость еще: self._z_characteristic, self.ep_reff_f = self.analyse_дисперсия( self.zl_eff, self.ep_reff, self.ep_r_f, w, s, h, собственная.частота.f) # анализируем потери линии self.alpha_conductor, self.alpha_dielectric = self.analyse_loss( реальный(self.ep_r_f), реальный(self.ep_reff_f), self.tand_f, ро, 1., собственная частота f, ш, т, с, лиц1, лиц1, лиц1)
def __str__(я) -> ул: f=собственная частота вывод = \ «Компланарные волноводные среды.
%i-%i %s. %i очков'%\ (f.f_scaled[0],f.f_scaled[-1],f.unit, f.npoints) + \ '\n W= %.2em, S= %.2em'% \ (я.ж, я.ы) возвратный вывод def __repr__(self) -> ул: вернуть себя.__str__() @имущество def Z0(self) -> NumberLike: """ Волновое сопротивление """ вернуть self._z_characteristic @имущество def gamma(self) -> NumberLike: """ Постоянная распространения. Возвращает ------- гамма: :класс:`numpy.ndarray` """ ep_reff, f = реальный (self.ep_reff_f), self.frequency.f альфа = self.alpha_dielectric.copy() если self.rho не None: альфа += self.alpha_conductor бета = 2. * pi * f * sqrt (ep_reff) / c вернуть альфа + 1j * бета
[документы] def analyse_dielectric(self, ep_r: NumberLike, tand: NumberLike, f_low: NumberLike, f_high: NumberLike, f_epr_tand: NumberLike, f: NumberLike, номер: ул): """ Эта функция вычисляет относительную диэлектрическую проницаемость, зависящую от частоты.
коэффициента диэлектрических и тангенциальных потерь. использованная литература ---------- .. [#] К. Свенссон, Г.Е. Дермер, Моделирование межсоединений с потерями во временной области, IEEE транс. по усовершенствованной упаковке, май 2001 г., N2, Vol. 24, стр. 191-196. .. [#] Джорджевич, Р.М. Билич, В.Д. Ликар-Смилянич, Т.К. Саркар, Широкополосная характеристика FR-4 в частотной области и во временной области причинность, IEEE транс. по ЭМС, вып. 43, №4, 2001, с. 662-667. Возвращает ------- ep_r_f::class:`numpy.ndarray` tand_f::class:`numpy.ndarray` """ if diel == 'djordjevicsvensson': # вычислить наклон для логарифмической шкалы частот, зависящий от tanD. k = log((f_high + 1j * f_epr_tand) / (f_low + 1j * f_epr_tand)) fd = log((f_high + 1j * f) / (f_low + 1j * f)) ep_d = -tand * ep_r / imag(k) # значение для частоты выше f_high ep_inf = ep_r * (1.
+ tand * real(k) / imag(k)) # вычислить комплексную диэлектрическую проницаемость ep_r_f = ep_inf + ep_d * fd # встать tand_f = -imag(ep_r_f) / реальный(ep_r_f) elif diel == 'частотный инвариант': ep_r_f = ep_r - 1j * ep_r * tand tand_f = tand еще: поднять ValueError('Неизвестная модель диэлектрической дисперсии') вернуть ep_r_f, tand_f
[документы] def analyse_quasi_static(self, ep_r: NumberLike, w: NumberLike, s: NumberLike, h: NumberLike, t: NumberLike, has_metal_backside: логическое значение): """ Эта функция вычисляет квазистатический импеданс компланарного волноводной линии, значение эффективной диэлектрической проницаемости по заполнению фактор, а эффективная ширина из-за конечной толщины проводника для заданных компланарных волноводных линий и свойств подложки.
Модель из [#]_ с воздушной спинкой и [#]_ с металлической спинкой. Модели скорректированы с учетом толщины полосы с использованием подхода первого порядка, описанного в [GGBB96]_. Отчет симулятора ADS для использования пользовательской коррекции на основе [Cohn60]_. Этот второй метод не реализован в skrf. использованная литература ---------- .. [GhNa84] Г. Гионе и К. Налди. "Аналитические формулы для копланарных прямых в гибридных и монолитных МИС», Electronics Letters, Том. 20, № 4, 16 февраля 1984 г., стр. 179-181. .. [GhNa83] Г. Гионе и К. Налди. "Параметры копланарных волноводов с Нижние общие плоскости», Electronics Letters, Том. 19, № 18, 1 сентября 1983 г., стр. 734-735. .. [Cohn60] SB Cohn, "Поправки на толщину для емкостных препятствий и Ленточные проводники», IRE Trans. on Microwave Theory and Techniques, Том. МТТ-8, ноябрь 1960 г.
, стр. 638-644. .. [GGBB96] KC Gupta, R. Garg, IJ Bahl, and P. Bhartia, Microstrip Линии и игровые линии, 2-е изд. Artech House, Inc., 1996. Возвращает ------- zl_eff::class:`numpy.ndarray` ep_reff::class:`numpy.ndarray` """ Z0 = кврт (mu_0 / эпсилон_0) а = ш б = ш + 2. * с # уравнение (3a) из [GhNa84] или (6) из [GhNa83] к1 = а/б kk1 = эллипсk(k1) kpk1 = эллипсk(sqrt(1. - k1 * k1)) q1 = эллипа (k1) # тыльная сторона металлическая если has_metal_backside: # уравнение (4) из [GhNa83] # в qucs коэффициент 2 превращается в 4 и лучше подходит для рекламы k3 = тангенс (пи * а / 4. / ч) / тангенс (пи * b / 4. / ч) q3 = эллипа (k3) qz = 1. / (q1 + q3) # уравнение (7) из [GhNa83] # эквивалентно e = (q1 + ep_r * q3) / (q1 + q3) и бумаге е = 1.
+ q3 * qz * (ep_r - 1.) # уравнение (8) из [GhNa83] с последующим делением на sqrt(e) zr = Z0 / 2. * qz # зад воздух еще: # уравнение (3b) из [GhNa84] k2 = sh((pi/4.) * a/h) / sh((pi/4.) * b/h) q2 = эллипа (k2) # уравнение (2) из [GhNa84] е = 1. + (ep_r - 1.) / 2. * q2 / q1 # уравнение (1) из [GhNa84] с последующим делением на sqrt(e) zr = Z0 / 4. / q1 # апостериорный эффект толщины полосы если t не None и t > 0.: # уравнение (7.98) из [GGBB96] d = 1,25 * t / pi * (1, + log (4, * pi * w / t)) # уравнение между (7.99) и (7.100) из [GGBB96] # ок. равно ke = (w + d) / (w + d + 2 * (s - d)) кэ = к1 + (1. - к1 * к1) * д / 2. / с qe = эллипа (ке) # тыльная сторона металлическая если has_metal_backside: # уравнение (8) из [GhNa83] с k1 -> ke # но оставить q3 без изменений ? (нет в газетах) qz = 1.
/ (qe + q3) zr = Z0 / 2. * qz # зад воздух еще: # уравнение (7.99) из [GGBB96] с последующим делением на sqrt(e) zr = Z0 / 4. / qe # изменяет ep_re # уравнение (7.100) из [GGBB96] e = e - (0,7 * (e - 1.) * t/s) / (q1 + (0,7 * t/s)) ep_reff = е # окончательное деление (1) от [GhNa84] и (8) от [GhNa83] zl_eff = zr / sqrt (ep_reff) return zl_eff, ep_reff, k1, kk1, kpk1
[документы] def analyse_diversion(self, zl_eff: NumberLike, ep_reff: NumberLike, ep_r: NumberLike, w: NumberLike, s: NumberLike, h: NumberLike, f: NumberLike): """ Эта функция вычисляет частотно-зависимую характеристику учет импеданса и эффективной диэлектрической проницаемости для компланарного волновода частотная дисперсия. использованная литература ---------- .
. [#] М. Ю. Франкель, С. Гупта, Дж. А. Вальдманис и Г. А. Муру, "Терагерцовые характеристики затухания и дисперсии компланарных Линии передачи» IEEE Trans. on Microwave Theory and Techniques, об. 39, нет. 6, стр. 910-916, июнь 1991 г. .. [#] С. Геворгян, Т. Мартинссон, А. Деленив, Э. Коллберг и И. Вендик, "Простое и точное дисперсионное выражение для эффективная диэлектрическая проницаемость копланарных волноводов» в Труды микроволн, антенн и распространения, об. 144, нет. 2. IEE, апрель 1997 г., стр. 145-148. Возвращает ------- z::class:`numpy.ndarray` e::class:`numpy.ndarray` """ # частота среза режима TE0 fte = ((c / 4.) / (h * sqrt (ep_r - 1.))) # коэффициент рассеивания G р = журнал (Вт / ч) и = 0,54 - (0,64 - 0,015 * р) * р v = 0,43 - (0,86 - 0,54 * р) * р G = exp(u * log(w/s) + v) # добавляем дисперсионные эффекты в ep_reff sqrt_ep_reff = sqrt(ep_reff) sqrt_e = sqrt_ep_reff + (sqrt(ep_r) - sqrt_ep_reff) / \ (1.
+ G * (f/fte)**(-1,8)) е = sqrt_e**2 z = zl_eff * sqrt_ep_reff / sqrt_e вернуть г, е
[документы] def analyse_loss(self, ep_r: NumberLike, ep_reff: NumberLike, tand: NumberLike, rho: NumberLike, mu_r: NumberLike, f: NumberLike, w: NumberLike, t: NumberLike, s: NumberLike, k1: NumberLike, kk1: NumberLike, kpk1: NumberLike): """ Функция рассчитывает потери в проводнике и диэлектрике компланарная волноводная линия с использованием правила приращения индуктивности Уилера. использованная литература ---------- .. [#] H.A. Wheeler, «Формулы скин-эффекта», Труды IRE, vol. 30, нет. 9, стр. 412-424, сентябрь 1942 г. .. [#] Г. Х. Оуян и Т. Т. Ву, "Приблизительные параметры слота Линии и их дополнение" Операции IRE по антеннам и Распространение, стр. 49-55, январь 1958 г.
def ellipa(k: NumberLike): """ Аппроксимация K(k)/K'(k). Впервые появился в [#]_ Более точные выражения можно найти в статье выше и в [#]_. Максимальная относительная погрешность реализованной здесь аппроксимации равна около 2 частей на миллион, что достаточно для любых практических целей. использованная литература ========== ... [#] G. Ghione, "Аналитическая модель, ориентированная на CAD, для потерь Общие асимметричные копланарные линии в гибридных и монолитных МИС» IEEE транс. по теории и технике микроволнового излучения, об. 41, нет. 9, стр. 1499-1510, сентябрь 1993 г. Возвращает ------- a_conductor::class:`numpy.ndarray` a_dielectric::class:`numpy.ndarray` """ Z0 = кврт (mu_0 / эпсилон_0) если t не None и t > 0.: если ро равно None: поднять(AttributeError('для расчета необходимо предоставить значения проводимости и толщины проводника. см. справку по инициализатору')) r_s = поверхностное_сопротивление (f = f, rho = rho, \ мю_р=1) ds = skin_depth (f = f, rho = rho, mu_r = 1.) если есть (t < 3 * ds): предупреждения.предупреждать( «Расчет потерь в проводнике недействителен для линии» 'высота t ({}) < 3 * глубина кожи ({})'.
format(t, ds[0]), Предупреждение во время выполнения ) n = (1. - k1) * 8. * pi / (t * (1. + k1)) а = ш/2. б = а + с ас = (пи + журнал (п * а)) / а + (пи + журнал (п * б)) / б a_conductor = r_s * sqrt(ep_reff) * ac / (4. * Z0 * kk1 * kpk1 * \ (1. - лиц.1 * лиц.1)) еще: a_conductor = нули (f.shape) l0 = с/f a_dielectric = pi * ep_r / (ep_r - 1) * (ep_reff - 1) / \ sqrt(ep_reff) * tand / l0 вернуть a_conductor, a_dielectric

 . частота импорт Частота
. частота импорт Частота

 По умолчанию — None (без коррекции ширины).
с учетом толщины полосы).
ep_r : число или массив
относительная диэлектрическая проницаемость диэлектрика на частоте f_epr_tand, ед.
mu_r : число, подобное массиву
относительная проницаемость мд диэлектрика, шт.
модель : ул.
микрополосковый квазистатический импеданс и диэлектрическая модель в:
* 'хаммерстадженсен' (по умолчанию)
* 'Шнайдер'
* 'Уилер'
дисп : ул
модель микрополоскового импеданса и диэлектрической частотной дисперсии в:
* 'хаммерстадженсен'
* 'киршнингянсен' (по умолчанию)
* 'кобаяси'
* 'Шнайдер'
* 'ямасита'
* 'никто'
номер : ул.
модель дисперсии диэлектрической частоты в:
* 'джорджевичсвенссон' (по умолчанию)
* 'частотно-инвариантный'
ро: число или массив, необязательно
Удельное сопротивление проводника, Ом/м
tand : число или массив
Коэффициент диэлектрических потерь на частоте f_epr_tand
rough : число или массив
Среднеквадратическая шероховатость проводника в м
f_low : число или массив
более низкая частота для широкополосного диэлектрика Дебая Джорджевича/Свенсона
модель, в Гц
f_high : число или массив
более высокая частота для широкополосного диэлектрика Дебая Джорджевича / Свенссона
модель, в Гц
f_epr_tand : число или массив
частота измерения ep_r и tand диэлектрика, Гц
compatibility_mode: str или None (по умолчанию)
Если установлено значение «qucs», происходит следующее поведение:
* Волновое сопротивление будет действительным (без мнимой части из-за tand)
* Квазистатические относительные диэлектрическая проницаемость и импеданс будут использоваться для
расчет потерь вместо частотно-дисперсионных значений
* Модели Кобаяши и Ямасита рассеивают диэлектрическую проницаемость, но сохраняют
значения квазистатического импеданса
\*args, \*\*kwargs : аргументы, аргументы ключевого слова
передается в конструктор :class:`~skrf.
По умолчанию — None (без коррекции ширины).
с учетом толщины полосы).
ep_r : число или массив
относительная диэлектрическая проницаемость диэлектрика на частоте f_epr_tand, ед.
mu_r : число, подобное массиву
относительная проницаемость мд диэлектрика, шт.
модель : ул.
микрополосковый квазистатический импеданс и диэлектрическая модель в:
* 'хаммерстадженсен' (по умолчанию)
* 'Шнайдер'
* 'Уилер'
дисп : ул
модель микрополоскового импеданса и диэлектрической частотной дисперсии в:
* 'хаммерстадженсен'
* 'киршнингянсен' (по умолчанию)
* 'кобаяси'
* 'Шнайдер'
* 'ямасита'
* 'никто'
номер : ул.
модель дисперсии диэлектрической частоты в:
* 'джорджевичсвенссон' (по умолчанию)
* 'частотно-инвариантный'
ро: число или массив, необязательно
Удельное сопротивление проводника, Ом/м
tand : число или массив
Коэффициент диэлектрических потерь на частоте f_epr_tand
rough : число или массив
Среднеквадратическая шероховатость проводника в м
f_low : число или массив
более низкая частота для широкополосного диэлектрика Дебая Джорджевича/Свенсона
модель, в Гц
f_high : число или массив
более высокая частота для широкополосного диэлектрика Дебая Джорджевича / Свенссона
модель, в Гц
f_epr_tand : число или массив
частота измерения ep_r и tand диэлектрика, Гц
compatibility_mode: str или None (по умолчанию)
Если установлено значение «qucs», происходит следующее поведение:
* Волновое сопротивление будет действительным (без мнимой части из-за tand)
* Квазистатические относительные диэлектрическая проницаемость и импеданс будут использоваться для
расчет потерь вместо частотно-дисперсионных значений
* Модели Кобаяши и Ямасита рассеивают диэлектрическую проницаемость, но сохраняют
значения квазистатического импеданса
\*args, \*\*kwargs : аргументы, аргументы ключевого слова
передается в конструктор :class:`~skrf.
 407-409., июнь 1980 г.
.. [#] М. Киршнинг и Р. Х. Янсен,
"Точная модель эффективной диэлектрической проницаемости микрополосковой полосы с
Действительность до частот миллиметрового диапазона », Electronics Letters,
об. 8, нет. 6, стр. 272-273, март 1982 г.
.. [#] Р. Х. Янсен и М. Киршнинг,
«Аргументы и точная модель силовой токовой формулировки
Характеристическое сопротивление микрополосковой полосы",
Archiv für Elektronik und Übertragungstechnik (AEÜ), vol. 37,
стр. 108-112, 1983.
.. [#] М. Кобаяши,
«Формула дисперсии, отвечающая последним требованиям к микрополосковым технологиям».
CAD", IEEE Trans. on Microwave Theory and Techniques, т. 36, № 8,
стр. 1246-1250, август 1988 г.
.. [#] М. В. Шнейдер,
"Микрополосковые линии для интегральных микросхем СВЧ",
Технический журнал Bell System, vol. 48, стр. 1421-1444, май 1969 г.
.. [#] М. В. Шнайдер, «Микрополосковая дисперсия», Труды IEEE,
Письма, том.
407-409., июнь 1980 г.
.. [#] М. Киршнинг и Р. Х. Янсен,
"Точная модель эффективной диэлектрической проницаемости микрополосковой полосы с
Действительность до частот миллиметрового диапазона », Electronics Letters,
об. 8, нет. 6, стр. 272-273, март 1982 г.
.. [#] Р. Х. Янсен и М. Киршнинг,
«Аргументы и точная модель силовой токовой формулировки
Характеристическое сопротивление микрополосковой полосы",
Archiv für Elektronik und Übertragungstechnik (AEÜ), vol. 37,
стр. 108-112, 1983.
.. [#] М. Кобаяши,
«Формула дисперсии, отвечающая последним требованиям к микрополосковым технологиям».
CAD", IEEE Trans. on Microwave Theory and Techniques, т. 36, № 8,
стр. 1246-1250, август 1988 г.
.. [#] М. В. Шнейдер,
"Микрополосковые линии для интегральных микросхем СВЧ",
Технический журнал Bell System, vol. 48, стр. 1421-1444, май 1969 г.
.. [#] М. В. Шнайдер, «Микрополосковая дисперсия», Труды IEEE,
Письма, том.
 по ЭМС, вып. 43, №4, 2001, с. 662-667.
"""
по ЭМС, вып. 43, №4, 2001, с. 662-667.
"""

 zl_eff, self.ep_reff, self.w_eff = self.analyse_quasi_static(
реальный (self.ep_r_f), self.w, self.h, self.t, self.model)
# в объявлениях используется комплексная диэлектрическая проницаемость, дающая комплексный импеданс и
# эффективная диэлектрическая проницаемость
еще:
self.zl_eff, self.ep_reff, self.w_eff = self.analyse_quasi_static(
self.ep_r_f, self.w, self.h, self.t, self.model)
# анализировать дисперсию импеданса и относительной диэлектрической проницаемости
# qucs использует w здесь, но w_eff кажется лучше
если compatibility_mode == 'qucs':
self._z_characteristic, self.ep_reff_f = self.analyse_дисперсия(
self.zl_eff, self.ep_reff, реальный (self.ep_r_f),
self.w, self.w_eff, self.h, self.t,
собственная частота.f, собственный дисплей)
еще:
self._z_characteristic, self.ep_reff_f = self.analyse_дисперсия(
self.
zl_eff, self.ep_reff, self.w_eff = self.analyse_quasi_static(
реальный (self.ep_r_f), self.w, self.h, self.t, self.model)
# в объявлениях используется комплексная диэлектрическая проницаемость, дающая комплексный импеданс и
# эффективная диэлектрическая проницаемость
еще:
self.zl_eff, self.ep_reff, self.w_eff = self.analyse_quasi_static(
self.ep_r_f, self.w, self.h, self.t, self.model)
# анализировать дисперсию импеданса и относительной диэлектрической проницаемости
# qucs использует w здесь, но w_eff кажется лучше
если compatibility_mode == 'qucs':
self._z_characteristic, self.ep_reff_f = self.analyse_дисперсия(
self.zl_eff, self.ep_reff, реальный (self.ep_r_f),
self.w, self.w_eff, self.h, self.t,
собственная частота.f, собственный дисплей)
еще:
self._z_characteristic, self.ep_reff_f = self.analyse_дисперсия(
self. zl_eff, self.ep_reff, self.ep_r_f,
self.w_eff, self.w_eff, self.h, self.t,
собственная частота.f, собственный дисплей)
# анализируем потери линии
# qucs использует здесь квазистатические значения, что приводит к разнице
# против рекламы
если compatibility_mode == 'qucs':
self.alpha_conductor, self.alpha_dielectric = self.analyse_loss(
реальный (self.ep_r_f), реальный (self.ep_reff), self.tand_f,
self.rho, self.mu_r,
реальный (self.zl_eff), реальный (self.zl_eff),
self.frequency.f, self.w, self.t, self.rough)
еще:
self.alpha_conductor, self.alpha_dielectric = self.analyse_loss(
реальный (self.ep_r_f), реальный (self.ep_reff_f), self.tand_f,
self.rho, self.mu_r,
реальный (self._z_characteristic), реальный (self._z_characteristic),
self.frequency.f, self.w, self.
zl_eff, self.ep_reff, self.ep_r_f,
self.w_eff, self.w_eff, self.h, self.t,
собственная частота.f, собственный дисплей)
# анализируем потери линии
# qucs использует здесь квазистатические значения, что приводит к разнице
# против рекламы
если compatibility_mode == 'qucs':
self.alpha_conductor, self.alpha_dielectric = self.analyse_loss(
реальный (self.ep_r_f), реальный (self.ep_reff), self.tand_f,
self.rho, self.mu_r,
реальный (self.zl_eff), реальный (self.zl_eff),
self.frequency.f, self.w, self.t, self.rough)
еще:
self.alpha_conductor, self.alpha_dielectric = self.analyse_loss(
реальный (self.ep_r_f), реальный (self.ep_reff_f), self.tand_f,
self.rho, self.mu_r,
реальный (self._z_characteristic), реальный (self._z_characteristic),
self.frequency.f, self.w, self. диэлектрических и тангенциальных потерь.
использованная литература
----------
.. [#] К. Свенссон, Г.Е. Дермер,
Моделирование межсоединений с потерями во временной области,
IEEE транс. по усовершенствованной упаковке, май 2001 г., N2, Vol. 24, стр. 191-196.
.. [#] Джорджевич, Р.М. Билич, В.Д. Ликар-Смилянич, Т.К. Саркар,
Широкополосная характеристика FR-4 в частотной области и во временной области
причинность,
IEEE транс. по ЭМС, вып. 43, №4, 2001, с. 662-667.
Возвращает
-------
ep_r_f::class:`numpy.ndarray`
tand_f::class:`numpy.ndarray`
"""
if diel == 'djordjevicsvensson':
# вычислить наклон для логарифмической шкалы частот, зависящий от tanD.
k = log((f_high + 1j * f_epr_tand) / (f_low + 1j * f_epr_tand))
fd = log((f_high + 1j * f) / (f_low + 1j * f))
ep_d = -tand * ep_r / imag(k)
# значение для частоты выше f_high
ep_inf = ep_r * (1.
диэлектрических и тангенциальных потерь.
использованная литература
----------
.. [#] К. Свенссон, Г.Е. Дермер,
Моделирование межсоединений с потерями во временной области,
IEEE транс. по усовершенствованной упаковке, май 2001 г., N2, Vol. 24, стр. 191-196.
.. [#] Джорджевич, Р.М. Билич, В.Д. Ликар-Смилянич, Т.К. Саркар,
Широкополосная характеристика FR-4 в частотной области и во временной области
причинность,
IEEE транс. по ЭМС, вып. 43, №4, 2001, с. 662-667.
Возвращает
-------
ep_r_f::class:`numpy.ndarray`
tand_f::class:`numpy.ndarray`
"""
if diel == 'djordjevicsvensson':
# вычислить наклон для логарифмической шкалы частот, зависящий от tanD.
k = log((f_high + 1j * f_epr_tand) / (f_low + 1j * f_epr_tand))
fd = log((f_high + 1j * f) / (f_low + 1j * f))
ep_d = -tand * ep_r / imag(k)
# значение для частоты выше f_high
ep_inf = ep_r * (1. + tand * real(k) / imag(k))
# вычислить комплексную диэлектрическую проницаемость
ep_r_f = ep_inf + ep_d * fd
# встать
tand_f = -imag(ep_r_f) / реальный(ep_r_f)
elif diel == 'частотный инвариант':
ep_r_f = ep_r - 1j * ep_r * tand
tand_f = tand
еще:
поднять ValueError('Неизвестная модель диэлектрической дисперсии')
вернуть ep_r_f, tand_f
+ tand * real(k) / imag(k))
# вычислить комплексную диэлектрическую проницаемость
ep_r_f = ep_inf + ep_d * fd
# встать
tand_f = -imag(ep_r_f) / реальный(ep_r_f)
elif diel == 'частотный инвариант':
ep_r_f = ep_r - 1j * ep_r * tand
tand_f = tand
еще:
поднять ValueError('Неизвестная модель диэлектрической дисперсии')
вернуть ep_r_f, tand_f  . [#] Э. Хаммерстад и Ø. Дженсен,
Симпозиум «Точные модели для автоматизированного проектирования микрополосковых шин».
по теории и технике микроволнового излучения, стр. 407-409., июнь 1980 г.
.. [#] Х. А. Уиллер,
«Свойства линии передачи полосы на диэлектрическом листе на
Самолет, IEEE Trans. по теории и технике микроволнового излучения, т. 1, с. 25,
нет. 8, стр. 631-647, август 1977 г.
.. [#] М. В. Шнейдер,
"Микрополосковые линии для интегральных микросхем СВЧ",
Технический журнал Bell System, vol. 48, стр. 1421-1444, май 1969 г.
Возвращает
-------
zl_eff::class:`numpy.ndarray`
ep_reff::class:`numpy.ndarray`
"""
Z0 = кврт (mu_0 / эпсилон_0)
zl_eff = Z0
ep_reff = ep_r
w_эфф = ш
если модель == 'колесо':
# вычислить эффект толщины полосы
дв1 = 0
если t не None и t > 0:
dw1 = t / pi * log (4.
. [#] Э. Хаммерстад и Ø. Дженсен,
Симпозиум «Точные модели для автоматизированного проектирования микрополосковых шин».
по теории и технике микроволнового излучения, стр. 407-409., июнь 1980 г.
.. [#] Х. А. Уиллер,
«Свойства линии передачи полосы на диэлектрическом листе на
Самолет, IEEE Trans. по теории и технике микроволнового излучения, т. 1, с. 25,
нет. 8, стр. 631-647, август 1977 г.
.. [#] М. В. Шнейдер,
"Микрополосковые линии для интегральных микросхем СВЧ",
Технический журнал Bell System, vol. 48, стр. 1421-1444, май 1969 г.
Возвращает
-------
zl_eff::class:`numpy.ndarray`
ep_reff::class:`numpy.ndarray`
"""
Z0 = кврт (mu_0 / эпсилон_0)
zl_eff = Z0
ep_reff = ep_r
w_эфф = ш
если модель == 'колесо':
# вычислить эффект толщины полосы
дв1 = 0
если t не None и t > 0:
dw1 = t / pi * log (4. * exp (1.) / sqrt ((t / h) ** 2) + \
(1. / pi / (вес / т + 1,1))**2)
dwr = (1. + 1. / ep_r) / 2. * dw1
вр = ш + двр
w_eff = wr
# вычислить волновое сопротивление
если (ш/ч) < 3,3:
cp = log(4. * h/wr + sqrt((4 * h/wr)**2 + 2))
b = (ep_r - 1.) / (ep_r + 1.) / \
2 * (лог(pi/2.) + log(4./pi)/ep_r)
zl_eff = (cp - b) * Z0 / pi / sqrt (2 * (ep_r + 1.))
еще:
cp = 1 + log(pi/2.) + log(wr/h/2. + 0,94)
d = 1. / pi / 2. * (1. + log(pi ** 2 / 16.)) * (ep_r - 1.) \
/ ep_r**2
x = 2. * log(2.) / pi + wr / h / 2. + (ep_r + 1.) / 2 / pi / \
ep_r * cp + d
zl_eff = Z0 / 2 / x / sqrt (ep_r)
# вычислить эффективную диэлектрическую проницаемость
если (ш/ч) < 1,3:
а = log(8 * ч/ч) + (ч/ч)**2/32
b = (ep_r - 1.
* exp (1.) / sqrt ((t / h) ** 2) + \
(1. / pi / (вес / т + 1,1))**2)
dwr = (1. + 1. / ep_r) / 2. * dw1
вр = ш + двр
w_eff = wr
# вычислить волновое сопротивление
если (ш/ч) < 3,3:
cp = log(4. * h/wr + sqrt((4 * h/wr)**2 + 2))
b = (ep_r - 1.) / (ep_r + 1.) / \
2 * (лог(pi/2.) + log(4./pi)/ep_r)
zl_eff = (cp - b) * Z0 / pi / sqrt (2 * (ep_r + 1.))
еще:
cp = 1 + log(pi/2.) + log(wr/h/2. + 0,94)
d = 1. / pi / 2. * (1. + log(pi ** 2 / 16.)) * (ep_r - 1.) \
/ ep_r**2
x = 2. * log(2.) / pi + wr / h / 2. + (ep_r + 1.) / 2 / pi / \
ep_r * cp + d
zl_eff = Z0 / 2 / x / sqrt (ep_r)
# вычислить эффективную диэлектрическую проницаемость
если (ш/ч) < 1,3:
а = log(8 * ч/ч) + (ч/ч)**2/32
b = (ep_r - 1. ) / (ep_r + 1.) / \
2 * (лог(pi/2.) + log(4./pi)/ep_r)
ep_reff = (ep_r + 1.) / 2. * (a / (a - b))**2
еще:
# qucsator 4.0137, но doc 0.94 * 2 = 1,88
d = (ep_r - 1.)/2./pi/ep_r*\
(log(2,1349 * wr/h + 4,0137) - 0,5169/ep_r)
e = wr / h / 2 + 1. / pi * log (8,5397 * wr / h + 16,0547)
ep_reff = ep_r * ((e - d) / e)**2
Элиф модель == 'Шнайдер':
и = ш / ч
дв = 0
# рассмотрим уравнения толщины полосы
если t не None и t > 0:
если t < (w/2):
если и < (1./пи/2):
аргумент = 2 * пи * вес / т
еще:
аргумент = ч / т
dw = t/pi * (1. + log(2 * arg))
если (t/dw) >= 0,75:
дв = 0
w_eff = w + dw
u = w_эфф/ч
# эффективная диэлектрическая проницаемость
ep_reff = (ep_r + 1.
) / (ep_r + 1.) / \
2 * (лог(pi/2.) + log(4./pi)/ep_r)
ep_reff = (ep_r + 1.) / 2. * (a / (a - b))**2
еще:
# qucsator 4.0137, но doc 0.94 * 2 = 1,88
d = (ep_r - 1.)/2./pi/ep_r*\
(log(2,1349 * wr/h + 4,0137) - 0,5169/ep_r)
e = wr / h / 2 + 1. / pi * log (8,5397 * wr / h + 16,0547)
ep_reff = ep_r * ((e - d) / e)**2
Элиф модель == 'Шнайдер':
и = ш / ч
дв = 0
# рассмотрим уравнения толщины полосы
если t не None и t > 0:
если t < (w/2):
если и < (1./пи/2):
аргумент = 2 * пи * вес / т
еще:
аргумент = ч / т
dw = t/pi * (1. + log(2 * arg))
если (t/dw) >= 0,75:
дв = 0
w_eff = w + dw
u = w_эфф/ч
# эффективная диэлектрическая проницаемость
ep_reff = (ep_r + 1. ) / 2. + (ep_r - 1.) / 2. / sqrt (1. + 10. / u)
# волновое сопротивление
если и < 1.:
z = 1./pi/2.*log(8./u + u/4)
еще:
z = 1. / (u + 2,42 - 0,44 / u + (1. - 1. / u)**6)
zl_eff = Z0 * z / sqrt (ep_reff)
Элиф модель == 'hammerstadjensen':
и = ш / ч
если t не None:
т = т/ч
ду1 = 0.
# вычислить эффект толщины полосы
если t не None и t > 0:
# Формула Qucs 11.22 неверна, вместо нее необходимо использовать нормализованную w (см. статью Hammerstad and Jensen)
# Нормализованный w называется u и фактически используется в исходном коде qucsator
# coth(альфа) = 1/tanh(альфа)
du1 = t / pi * log(1. + 4. * exp(1.) / t * tanh(sqrt(6.517 * u))**2)
# sech(альфа) = 1/cosh(альфа)
dur = du1 * (1. + 1. / ch(sqrt(ep_r - 1.
) / 2. + (ep_r - 1.) / 2. / sqrt (1. + 10. / u)
# волновое сопротивление
если и < 1.:
z = 1./pi/2.*log(8./u + u/4)
еще:
z = 1. / (u + 2,42 - 0,44 / u + (1. - 1. / u)**6)
zl_eff = Z0 * z / sqrt (ep_reff)
Элиф модель == 'hammerstadjensen':
и = ш / ч
если t не None:
т = т/ч
ду1 = 0.
# вычислить эффект толщины полосы
если t не None и t > 0:
# Формула Qucs 11.22 неверна, вместо нее необходимо использовать нормализованную w (см. статью Hammerstad and Jensen)
# Нормализованный w называется u и фактически используется в исходном коде qucsator
# coth(альфа) = 1/tanh(альфа)
du1 = t / pi * log(1. + 4. * exp(1.) / t * tanh(sqrt(6.517 * u))**2)
# sech(альфа) = 1/cosh(альфа)
dur = du1 * (1. + 1. / ch(sqrt(ep_r - 1. ))) / 2.
и1 = и + du1
ур = и + продолжительность
w_eff = ур * ч
# вычислить импеданс для однородной среды
zr = хаммерстад_zl (ур)
z1 = хаммерстад_zl(u1)
# вычислить эффективную диэлектрическую проницаемость
a, b = Hammerstad_ab(ur, ep_r)
e = Hammerstad_er (ur, ep_r, a, b)
# вычислить окончательный характеристический импеданс и диэлектрическую проницаемость
# включая эффекты толщины полосы
zl_eff = zr / sqrt(e)
ep_reff = e * (z1 / zr)**2
еще:
поднять ValueError('Неизвестная квазистатическая модель микрополосковой линии')
вернуть zl_eff, ep_reff, w_eff
))) / 2.
и1 = и + du1
ур = и + продолжительность
w_eff = ур * ч
# вычислить импеданс для однородной среды
zr = хаммерстад_zl (ур)
z1 = хаммерстад_zl(u1)
# вычислить эффективную диэлектрическую проницаемость
a, b = Hammerstad_ab(ur, ep_r)
e = Hammerstad_er (ur, ep_r, a, b)
# вычислить окончательный характеристический импеданс и диэлектрическую проницаемость
# включая эффекты толщины полосы
zl_eff = zr / sqrt(e)
ep_reff = e * (z1 / zr)**2
еще:
поднять ValueError('Неизвестная квазистатическая модель микрополосковой линии')
вернуть zl_eff, ep_reff, w_eff  использованная литература
----------
.. [#] М. Кобаяши,
«Формула дисперсии, отвечающая последним требованиям к микрополосковым технологиям».
CAD", IEEE Trans. on Microwave Theory and Techniques, vol. 36,
нет. 8, стр. 1246-1250, 19 августа.88.
.. [#] М. В. Шнайдер, "Микрополосковая дисперсия", Труды
IEEE, письма, том. 60, январь 1972 г., стр. 144–146.
.. [#] М. Киршнинг и Р. Х. Янсен,
«Точная модель эффективной диэлектрической проницаемости микрополоскового
с достоверностью до частот миллиметрового диапазона", Электроника
Письма, том. 8, нет. 6, стр. 272-273, март 1982 г.
.. [#] Р. Х. Янсен и М. Киршнинг,
«Аргументы и точная модель силовой токовой формулировки
Характеристическое сопротивление микрополосковой полосы",
Archiv für Elektronik und Übertragungstechnik (AEÜ), vol. 37,
стр. 108-112, 1983.
использованная литература
----------
.. [#] М. Кобаяши,
«Формула дисперсии, отвечающая последним требованиям к микрополосковым технологиям».
CAD", IEEE Trans. on Microwave Theory and Techniques, vol. 36,
нет. 8, стр. 1246-1250, 19 августа.88.
.. [#] М. В. Шнайдер, "Микрополосковая дисперсия", Труды
IEEE, письма, том. 60, январь 1972 г., стр. 144–146.
.. [#] М. Киршнинг и Р. Х. Янсен,
«Точная модель эффективной диэлектрической проницаемости микрополоскового
с достоверностью до частот миллиметрового диапазона", Электроника
Письма, том. 8, нет. 6, стр. 272-273, март 1982 г.
.. [#] Р. Х. Янсен и М. Киршнинг,
«Аргументы и точная модель силовой токовой формулировки
Характеристическое сопротивление микрополосковой полосы",
Archiv für Elektronik und Übertragungstechnik (AEÜ), vol. 37,
стр. 108-112, 1983. .. [#] Э. Ямасита, К. Ацуки и Т. Уэда,
"Примерная дисперсионная формула микрополосковых линий для
Компьютерное проектирование интегральных схем СВЧ",
IEEE транс. по теории и технике микроволнового излучения, т. 1, с. 27,
стр. 1036-1038, декабрь 1979 г.
Возвращает
-------
z::class:`numpy.ndarray`
e::class:`numpy.ndarray`
"""
u = Вт/ч
если дисп == 'Шнайдер':
k = sqrt (ep_reff / ep_r)
fn = 4. * h * f / c * sqrt (ep_r - 1.)
фн2 = фн**2
e = ep_ref * ((1. + fn2) / (1. + k * fn2))**2
z = zl_eff * sqrt (ep_reff / e)
elif disp == 'hammerstadjensen':
Z0 = кврт (mu_0 / эпсилон_0)
g = pi**2 / 12 * (ep_r - 1) / ep_reff * sqrt (2 * pi * zl_eff / Z0)
fp = (2 * mu_0 * h * f) / zl_eff
e = ep_r - (ep_r - ep_reff) / (1 + g * fp**2)
z = zl_eff * sqrt (ep_reff / e) * (e - 1) / (ep_reff - 1)
Элиф дисп == 'киршнингянсен':
фн = ф * ч * 1е-6
e = kirsching_er (u, fn, ep_r, ep_reff)
z, _ = kirsching_zl(u, fn, ep_r, ep_reff, e, zl_eff)
Элиф дисп == 'ямасита':
k = sqrt (ep_r / ep_reff)
fp = 4 * h * f / c * sqrt (ep_r - 1) * \
(0,5 + (1 + 2 * log10(1 + u))**2)
e = ep_reff * ((1 + k * fp**1,5/4) / (1 + fp**1,5/4))**2
# qucs сохраняет здесь квазистатический импеданс
если self.
.. [#] Э. Ямасита, К. Ацуки и Т. Уэда,
"Примерная дисперсионная формула микрополосковых линий для
Компьютерное проектирование интегральных схем СВЧ",
IEEE транс. по теории и технике микроволнового излучения, т. 1, с. 27,
стр. 1036-1038, декабрь 1979 г.
Возвращает
-------
z::class:`numpy.ndarray`
e::class:`numpy.ndarray`
"""
u = Вт/ч
если дисп == 'Шнайдер':
k = sqrt (ep_reff / ep_r)
fn = 4. * h * f / c * sqrt (ep_r - 1.)
фн2 = фн**2
e = ep_ref * ((1. + fn2) / (1. + k * fn2))**2
z = zl_eff * sqrt (ep_reff / e)
elif disp == 'hammerstadjensen':
Z0 = кврт (mu_0 / эпсилон_0)
g = pi**2 / 12 * (ep_r - 1) / ep_reff * sqrt (2 * pi * zl_eff / Z0)
fp = (2 * mu_0 * h * f) / zl_eff
e = ep_r - (ep_r - ep_reff) / (1 + g * fp**2)
z = zl_eff * sqrt (ep_reff / e) * (e - 1) / (ep_reff - 1)
Элиф дисп == 'киршнингянсен':
фн = ф * ч * 1е-6
e = kirsching_er (u, fn, ep_r, ep_reff)
z, _ = kirsching_zl(u, fn, ep_r, ep_reff, e, zl_eff)
Элиф дисп == 'ямасита':
k = sqrt (ep_r / ep_reff)
fp = 4 * h * f / c * sqrt (ep_r - 1) * \
(0,5 + (1 + 2 * log10(1 + u))**2)
e = ep_reff * ((1 + k * fp**1,5/4) / (1 + fp**1,5/4))**2
# qucs сохраняет здесь квазистатический импеданс
если self.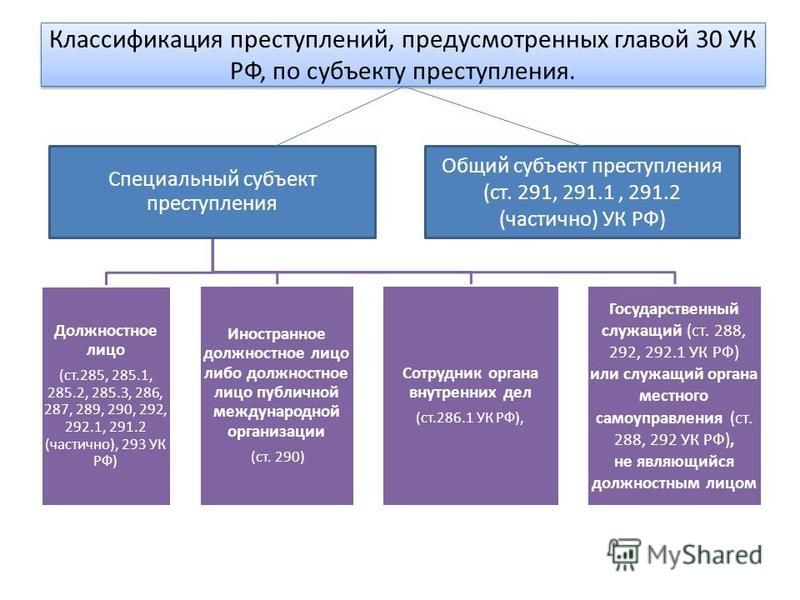 compatibility_mode == 'qucs':
z = npy.ones (f.shape) * zl_eff
# по умолчанию использовать Kirschning Jansen для дисперсии импеданса
еще:
фн = ф * ч * 1е-6
z, _ = kirsching_zl(wr/h, fn, ep_r, ep_reff, e, zl_eff)
Элиф дисп == 'кобаяши':
fk = c * arctan(ep_r * sqrt((ep_reff - 1) / (ep_r - ep_reff)))/ \
(2 * pi * h * sqrt (ep_r - ep_reff))
fh = fk / (0,75 + (0,75 - 0,332 / (ep_r**1,73)) * u)
нет = 1 + 1 / (1 + sqrt(u)) + 0,32 * (1 / (1 + sqrt(u))**3
nc = npy.where(u < 0,7,
1 + 1,4 / (1 + u) * (0,15 - 0,235 * exp (-0,45 * f / fh)),
1)
n = npy.where (нет * nc < 2,32, нет * nc, 2,32)
e = ep_r - (ep_r - ep_reff) / (1 + (f / fh)**n)
# qucs сохраняет здесь квазистатический импеданс
если self.compatibility_mode == 'qucs':
z = npy.ones (f.shape) * zl_eff
# по умолчанию использовать Kirschning Jansen для дисперсии импеданса
еще:
фн = ф * ч * 1е-6
z, _ = kirsching_zl(wr/h, fn, ep_r, ep_reff, e, zl_eff)
Элиф дисп == 'нет':
e = единицы (f.
compatibility_mode == 'qucs':
z = npy.ones (f.shape) * zl_eff
# по умолчанию использовать Kirschning Jansen для дисперсии импеданса
еще:
фн = ф * ч * 1е-6
z, _ = kirsching_zl(wr/h, fn, ep_r, ep_reff, e, zl_eff)
Элиф дисп == 'кобаяши':
fk = c * arctan(ep_r * sqrt((ep_reff - 1) / (ep_r - ep_reff)))/ \
(2 * pi * h * sqrt (ep_r - ep_reff))
fh = fk / (0,75 + (0,75 - 0,332 / (ep_r**1,73)) * u)
нет = 1 + 1 / (1 + sqrt(u)) + 0,32 * (1 / (1 + sqrt(u))**3
nc = npy.where(u < 0,7,
1 + 1,4 / (1 + u) * (0,15 - 0,235 * exp (-0,45 * f / fh)),
1)
n = npy.where (нет * nc < 2,32, нет * nc, 2,32)
e = ep_r - (ep_r - ep_reff) / (1 + (f / fh)**n)
# qucs сохраняет здесь квазистатический импеданс
если self.compatibility_mode == 'qucs':
z = npy.ones (f.shape) * zl_eff
# по умолчанию использовать Kirschning Jansen для дисперсии импеданса
еще:
фн = ф * ч * 1е-6
z, _ = kirsching_zl(wr/h, fn, ep_r, ep_reff, e, zl_eff)
Элиф дисп == 'нет':
e = единицы (f. shape) * ep_reff
z = единицы (f.shape) * zl_eff
еще:
поднять ValueError('Неизвестная модель микрополосковой дисперсии')
вернуть г, е
shape) * ep_reff
z = единицы (f.shape) * zl_eff
еще:
поднять ValueError('Неизвестная модель микрополосковой дисперсии')
вернуть г, е  ndarray`
"""
# ограничено только моделями Hammerstad и Jensen
Z0 = npy.sqrt (mu_0/epsilon_0)
# потери в проводнике
если t не None и t > 0:
если ро равно None:
поднять(AttributeError('должно быть указано удельное сопротивление rho. '
'см. справку по инициализатору'))
еще:
Rs = поверхностное_сопротивление (f = f, rho = rho, mu_r = 1)
ds = глубина кожи (f, rho, mu_r)
если (npy.any (t < 3 * ds)):
предупреждения.предупреждать(
«Расчет потерь в проводнике недействителен для линии»
'высота t ({}) < 3 * глубина кожи ({})'.format(t, ds[0]),
Предупреждение во время выполнения
)
# текущий коэффициент распределения
Ki = exp(-1,2 * ((zl_eff_f1 + zl_eff_f2) / 2 / Z0)**0,7)
# D – среднеквадратическая шероховатость поверхности.
ndarray`
"""
# ограничено только моделями Hammerstad и Jensen
Z0 = npy.sqrt (mu_0/epsilon_0)
# потери в проводнике
если t не None и t > 0:
если ро равно None:
поднять(AttributeError('должно быть указано удельное сопротивление rho. '
'см. справку по инициализатору'))
еще:
Rs = поверхностное_сопротивление (f = f, rho = rho, mu_r = 1)
ds = глубина кожи (f, rho, mu_r)
если (npy.any (t < 3 * ds)):
предупреждения.предупреждать(
«Расчет потерь в проводнике недействителен для линии»
'высота t ({}) < 3 * глубина кожи ({})'.format(t, ds[0]),
Предупреждение во время выполнения
)
# текущий коэффициент распределения
Ki = exp(-1,2 * ((zl_eff_f1 + zl_eff_f2) / 2 / Z0)**0,7)
# D – среднеквадратическая шероховатость поверхности. Kr = 1 + 2 / pi * arctan (1,4 * (D/ds)**2)
a_проводник = Rs / (zl_eff_f1 * w) * Ki * Kr
еще:
a_conductor = нули (f.shape)
# диэлектрические потери
l0 = с/f
a_dielectric = pi * ep_r / (ep_r - 1) * (ep_reff - 1) / \
sqrt(ep_reff) * tand / l0
вернуть a_conductor, a_dielectric
Kr = 1 + 2 / pi * arctan (1,4 * (D/ds)**2)
a_проводник = Rs / (zl_eff_f1 * w) * Ki * Kr
еще:
a_conductor = нули (f.shape)
# диэлектрические потери
l0 = с/f
a_dielectric = pi * ep_r / (ep_r - 1) * (ep_reff - 1) / \
sqrt(ep_reff) * tand / l0
вернуть a_conductor, a_dielectric  """
return (ep_r + 1) / 2 + (ep_r - 1) / 2 * (1. + 10. / u)**(-a * b)
def kirsching_zl(u: NumberLike, fn: NumberLike,
ep_r: NumberLike, ep_reff: NumberLike, ep_reff_f: NumberLike,
zl_eff: число лайков):
"""
Дисперсия импеданса Киршнинг-Янсена.
"""
#fn = f * h * 1e-6 # ГГц-мм
R1 = npy.минимум (0,03891 * воз_р**1,4, 20.)
R2 = npy.минимум (0,2671 * u**7, 20.)
R3 = 4,766 * ехр (-3,228 * u**0,641)
R4 = 0,016 + (0,0514 * ep_r)**4,524
R5 = (фн / 28,843)**12
R6 = npy.минимум (22,20 * u ** 1,92, 20.)
R7 = 1,206 - 0,3144 * exp(-R1) * (1 - exp(-R2))
R8 = 1 + 1,275 * (1 - exp(-0,004625 * R3 * ep_r**1,674 \
* (фн / 18,365)**2,745))
R9 = 5,086 * R4 * R5/(0,3838 + 0,386 * R4) \
* ехр(-R6) / (1 + 1,2992 * R5) \
* (ep_r - 1)**6 / (1 + 10 * (ep_r - 1)**6)
R10 = 0,00044 * ep_r** 2,136 + 0,0184
Р11 = (лн/190,47)**6 / (1 + 0,0962 * (фн / 19,47)**6)
R12 = 1 / (1 + 0,00245 * u**2)
R13 = 0,9408 * ep_reff_f**R8 - 0,9603
R14 = (0,9408 - R9) * ep_reff**R8 - 0,9603
R15 = 0,707 * R10 * (фн / 12,3)**1,097
R16 = 1 + 0,0503 * ep_r**2 * R11 * (1 - exp(-(u / 15)**6))
R17 = R7 * (1 - 1,1241 * R12 / R16 \
*exp(-0,026 * fn**1,15656 - R15))
возврат zl_eff * (R13/R14)**R17, R17
def kirsching_er(u: NumberLike, fn: NumberLike,
ep_r: NumberLike, ep_reff: NumberLike):
"""
Дисперсия относительной диэлектрической проницаемости Киршнинг-Янсена.
"""
return (ep_r + 1) / 2 + (ep_r - 1) / 2 * (1. + 10. / u)**(-a * b)
def kirsching_zl(u: NumberLike, fn: NumberLike,
ep_r: NumberLike, ep_reff: NumberLike, ep_reff_f: NumberLike,
zl_eff: число лайков):
"""
Дисперсия импеданса Киршнинг-Янсена.
"""
#fn = f * h * 1e-6 # ГГц-мм
R1 = npy.минимум (0,03891 * воз_р**1,4, 20.)
R2 = npy.минимум (0,2671 * u**7, 20.)
R3 = 4,766 * ехр (-3,228 * u**0,641)
R4 = 0,016 + (0,0514 * ep_r)**4,524
R5 = (фн / 28,843)**12
R6 = npy.минимум (22,20 * u ** 1,92, 20.)
R7 = 1,206 - 0,3144 * exp(-R1) * (1 - exp(-R2))
R8 = 1 + 1,275 * (1 - exp(-0,004625 * R3 * ep_r**1,674 \
* (фн / 18,365)**2,745))
R9 = 5,086 * R4 * R5/(0,3838 + 0,386 * R4) \
* ехр(-R6) / (1 + 1,2992 * R5) \
* (ep_r - 1)**6 / (1 + 10 * (ep_r - 1)**6)
R10 = 0,00044 * ep_r** 2,136 + 0,0184
Р11 = (лн/190,47)**6 / (1 + 0,0962 * (фн / 19,47)**6)
R12 = 1 / (1 + 0,00245 * u**2)
R13 = 0,9408 * ep_reff_f**R8 - 0,9603
R14 = (0,9408 - R9) * ep_reff**R8 - 0,9603
R15 = 0,707 * R10 * (фн / 12,3)**1,097
R16 = 1 + 0,0503 * ep_r**2 * R11 * (1 - exp(-(u / 15)**6))
R17 = R7 * (1 - 1,1241 * R12 / R16 \
*exp(-0,026 * fn**1,15656 - R15))
возврат zl_eff * (R13/R14)**R17, R17
def kirsching_er(u: NumberLike, fn: NumberLike,
ep_r: NumberLike, ep_reff: NumberLike):
"""
Дисперсия относительной диэлектрической проницаемости Киршнинг-Янсена. """
# в документе fn выражена в ГГц-см, а в Qucs - ГГц-мм, таким образом, коэффициент
# 10 для всех констант, которые умножают или делят fn
P1 = 0,27488 + (0,6315 + 0,525 / ( 1+ 0,0157 * fn)**20) * u \
-0,065683 * ехр (-8,7513 * и)
P2 = 0,33622 * (1 -exp(-0,03442 * ep_r))
P3 = 0,0363 * exp (-4,6 * u) * (1 - exp (- (fn / 38,7) ** 4,97))
P4 = 1 + 2,751 * (1 - exp(-(ep_r / 15,916)**8))
Pf = P1 * P2 * ((0,1844 + P3 * P4) * fn)**1,5763
вернуть ep_r - (ep_r - ep_reff) / (1 + Pf)
"""
# в документе fn выражена в ГГц-см, а в Qucs - ГГц-мм, таким образом, коэффициент
# 10 для всех констант, которые умножают или делят fn
P1 = 0,27488 + (0,6315 + 0,525 / ( 1+ 0,0157 * fn)**20) * u \
-0,065683 * ехр (-8,7513 * и)
P2 = 0,33622 * (1 -exp(-0,03442 * ep_r))
P3 = 0,0363 * exp (-4,6 * u) * (1 - exp (- (fn / 38,7) ** 4,97))
P4 = 1 + 2,751 * (1 - exp(-(ep_r / 15,916)**8))
Pf = P1 * P2 * ((0,1844 + P3 * P4) * fn)**1,5763
вернуть ep_r - (ep_r - ep_reff) / (1 + Pf)
 . частота импорт Частота
. частота импорт Частота Квазистатические модели волнового сопротивления и эффективного
диэлектрическая проницаемость дает значение при нулевой частоте. Дисперсионные модели
вычислить частотно-зависимые значения этих переменных.
* Модель квазистатического волнового сопротивления и эффективной диэлектрической проницаемости
используйте [GhNa84]_ и [GhNa83]_. Модели скорректированы с учетом
толщины полосы с использованием подхода первого порядка, описанного в [GGBB96]_.
Сравнение показывает, что симулятор ADS использует другую коррекцию толщины.
метод, соответствующий документу ADS, основанному на [Cohn60]_. Этот второй метод
не реализован в skrf.
* Использование модели частотной дисперсии импеданса и эффективной диэлектрической проницаемости
[FGVM91]_ и [GMDK97]_.
* Модель потерь рассчитана с использованием правила приращения индуктивности Уилера.
[Whee42]_ применяется к копланарному волноводу [OwWu58]_ и [Ghio93]_.
Параметры
----------
частота : :class:`~skrf.
Квазистатические модели волнового сопротивления и эффективного
диэлектрическая проницаемость дает значение при нулевой частоте. Дисперсионные модели
вычислить частотно-зависимые значения этих переменных.
* Модель квазистатического волнового сопротивления и эффективной диэлектрической проницаемости
используйте [GhNa84]_ и [GhNa83]_. Модели скорректированы с учетом
толщины полосы с использованием подхода первого порядка, описанного в [GGBB96]_.
Сравнение показывает, что симулятор ADS использует другую коррекцию толщины.
метод, соответствующий документу ADS, основанному на [Cohn60]_. Этот второй метод
не реализован в skrf.
* Использование модели частотной дисперсии импеданса и эффективной диэлектрической проницаемости
[FGVM91]_ и [GMDK97]_.
* Модель потерь рассчитана с использованием правила приращения индуктивности Уилера.
[Whee42]_ применяется к копланарному волноводу [OwWu58]_ и [Ghio93]_.
Параметры
----------
частота : :class:`~skrf. frequency.Frequency` объект, необязательный
полоса частот носителя. По умолчанию нет.
z0 : число, массив или None (по умолчанию None)
импеданс порта для среды. Требуется только в том случае, если отличается от
волновое сопротивление Z0 линии передачи. в омах
w : число или массив
ширина центральной жилы, м. По умолчанию 3e-3 м.
s : число или массив
шаг (ширина зазора), м. По умолчанию 0,3e-3 м.
h : число или массив
высота подложки между тыльной стороной и проводником, м.
По умолчанию 1,55 м (эквивалентно бесконечной высоте для w и s по умолчанию).
t : число или массив, необязательный
толщина проводника, м. По умолчанию — None (без коррекции ширины).
для учета толщины полосы).
has_metal_backside : bool, по умолчанию False
Если обратная сторона воздушная (ложь) или металлическая (правда)
ep_r : число или массив, необязательный
относительная диэлектрическая проницаемость подложки на частоте f_epr_tand,
нет единицы.
frequency.Frequency` объект, необязательный
полоса частот носителя. По умолчанию нет.
z0 : число, массив или None (по умолчанию None)
импеданс порта для среды. Требуется только в том случае, если отличается от
волновое сопротивление Z0 линии передачи. в омах
w : число или массив
ширина центральной жилы, м. По умолчанию 3e-3 м.
s : число или массив
шаг (ширина зазора), м. По умолчанию 0,3e-3 м.
h : число или массив
высота подложки между тыльной стороной и проводником, м.
По умолчанию 1,55 м (эквивалентно бесконечной высоте для w и s по умолчанию).
t : число или массив, необязательный
толщина проводника, м. По умолчанию — None (без коррекции ширины).
для учета толщины полосы).
has_metal_backside : bool, по умолчанию False
Если обратная сторона воздушная (ложь) или металлическая (правда)
ep_r : число или массив, необязательный
относительная диэлектрическая проницаемость подложки на частоте f_epr_tand,
нет единицы. По умолчанию 4,5.
номер : ул.
модель дисперсии диэлектрической частоты в:
* 'джорджевичсвенссон' (по умолчанию)
* 'частотно-инвариантный'
rho : число, или массив, или None
Удельное сопротивление проводника, Ом/м. По умолчанию 1,68e-8 Ом/м (медь).
tand : число или массив
коэффициент диэлектрических потерь на частоте f_epr_tand. По умолчанию 0.
f_low : число или массив
более низкая частота для широкополосного диэлектрика Дебая Джорджевича/Свенсона
модель, в Гц. По умолчанию 1 кГц.
f_high : число или массив
более высокая частота для широкополосного диэлектрика Дебая Джорджевича / Свенссона
модель, в Гц. По умолчанию 1 ТГц.
f_epr_tand : число или массив
частота измерения ep_r и tand диэлектрика, Гц.
По умолчанию 1 ГГц.
compatibility_mode: str или None (по умолчанию)
Если установлено значение «qucs», происходит следующее поведение:
* Волновое сопротивление будет действительным (без мнимой части из-за tand)
\*args, \*\*kwargs : аргументы, аргументы ключевого слова
передается в конструктор :class:`~skrf.
По умолчанию 4,5.
номер : ул.
модель дисперсии диэлектрической частоты в:
* 'джорджевичсвенссон' (по умолчанию)
* 'частотно-инвариантный'
rho : число, или массив, или None
Удельное сопротивление проводника, Ом/м. По умолчанию 1,68e-8 Ом/м (медь).
tand : число или массив
коэффициент диэлектрических потерь на частоте f_epr_tand. По умолчанию 0.
f_low : число или массив
более низкая частота для широкополосного диэлектрика Дебая Джорджевича/Свенсона
модель, в Гц. По умолчанию 1 кГц.
f_high : число или массив
более высокая частота для широкополосного диэлектрика Дебая Джорджевича / Свенссона
модель, в Гц. По умолчанию 1 ТГц.
f_epr_tand : число или массив
частота измерения ep_r и tand диэлектрика, Гц.
По умолчанию 1 ГГц.
compatibility_mode: str или None (по умолчанию)
Если установлено значение «qucs», происходит следующее поведение:
* Волновое сопротивление будет действительным (без мнимой части из-за tand)
\*args, \*\*kwargs : аргументы, аргументы ключевого слова
передается в конструктор :class:`~skrf. media.media.Media`
(:func:`~skrf.media.media.Media.__init__`
Примечание
----
При толщине полосы менее 3 толщин скин-слоя потери
модель дает чрезмерно оптимистичные результаты, и средства массовой информации вынесут предупреждение.
При постоянном токе потери в линии могут быть меньше, чем в ее проводнике.
сопротивление, которое не является физическим.
использованная литература
----------
.. [QUCSa] http://qucs.sourceforge.net/docs/technical.pdf
.. [QUCSb] http://www.qucs.sourceforge.net/
.. [DBLS01] Джорджевич, Р.М. Билич, В.Д. Ликар-Смилянич, Т.К. Саркар,
Широкополосная характеристика FR-4 в частотной области и во временной области
причинность,
IEEE транс. по ЭМС, вып. 43, №4, 2001, с. 662-667.
.. [SvDe01] К. Свенссон, Г.Е. Дермер,
Моделирование межсоединений с потерями во временной области,
IEEE транс. по усовершенствованной упаковке, май 2001 г., N2, Vol. 24, стр. 191-196.
media.media.Media`
(:func:`~skrf.media.media.Media.__init__`
Примечание
----
При толщине полосы менее 3 толщин скин-слоя потери
модель дает чрезмерно оптимистичные результаты, и средства массовой информации вынесут предупреждение.
При постоянном токе потери в линии могут быть меньше, чем в ее проводнике.
сопротивление, которое не является физическим.
использованная литература
----------
.. [QUCSa] http://qucs.sourceforge.net/docs/technical.pdf
.. [QUCSb] http://www.qucs.sourceforge.net/
.. [DBLS01] Джорджевич, Р.М. Билич, В.Д. Ликар-Смилянич, Т.К. Саркар,
Широкополосная характеристика FR-4 в частотной области и во временной области
причинность,
IEEE транс. по ЭМС, вып. 43, №4, 2001, с. 662-667.
.. [SvDe01] К. Свенссон, Г.Е. Дермер,
Моделирование межсоединений с потерями во временной области,
IEEE транс. по усовершенствованной упаковке, май 2001 г., N2, Vol. 24, стр. 191-196. .. [GhNa84] Г. Гионе и К. Налди. "Аналитические формулы для копланарных прямых
в гибридных и монолитных МИС», Electronics Letters,
Том. 20, № 4, 16 февраля 1984 г., стр. 179-181.
.. [GhNa83] Г. Гионе и К. Налди. "Параметры копланарных волноводов с
Нижние общие плоскости», Electronics Letters,
Том. 19, № 18, 1 сентября 1983 г., стр. 734-735.
.. [Cohn60] SB Cohn, "Поправки на толщину для емкостных препятствий и
Ленточные проводники», IRE Trans. on Microwave Theory and Techniques,
Том. МТТ-8, 19 ноября60, стр. 638-644.
.. [GGBB96] KC Gupta, R. Garg, IJ Bahl, and P. Bhartia, Microstrip
Линии и игровые линии, 2-е изд. Artech House, Inc., 1996.
.. [FGVM91] М. Ю. Франкель, С. Гупта, Дж. А. Вальдманис и Г. А. Муру,
"Терагерцовые характеристики затухания и дисперсии компланарных
Линии передачи» IEEE Trans. on Microwave Theory and Techniques,
об. 39, нет. 6, стр. 910-916, июнь 1991 г.
.. [GMDK97] С. Геворгян, Т.
.. [GhNa84] Г. Гионе и К. Налди. "Аналитические формулы для копланарных прямых
в гибридных и монолитных МИС», Electronics Letters,
Том. 20, № 4, 16 февраля 1984 г., стр. 179-181.
.. [GhNa83] Г. Гионе и К. Налди. "Параметры копланарных волноводов с
Нижние общие плоскости», Electronics Letters,
Том. 19, № 18, 1 сентября 1983 г., стр. 734-735.
.. [Cohn60] SB Cohn, "Поправки на толщину для емкостных препятствий и
Ленточные проводники», IRE Trans. on Microwave Theory and Techniques,
Том. МТТ-8, 19 ноября60, стр. 638-644.
.. [GGBB96] KC Gupta, R. Garg, IJ Bahl, and P. Bhartia, Microstrip
Линии и игровые линии, 2-е изд. Artech House, Inc., 1996.
.. [FGVM91] М. Ю. Франкель, С. Гупта, Дж. А. Вальдманис и Г. А. Муру,
"Терагерцовые характеристики затухания и дисперсии компланарных
Линии передачи» IEEE Trans. on Microwave Theory and Techniques,
об. 39, нет. 6, стр. 910-916, июнь 1991 г.
.. [GMDK97] С. Геворгян, Т. Мартинссон, А. Деленив, Э. Коллберг и
И. Вендик, "Простое и точное дисперсионное выражение для
эффективная диэлектрическая проницаемость копланарных волноводов» в
Труды микроволн, антенн и распространения,
об. 144, нет. 2. IEE, 19 апреля.97, стр. 145-148.
.. [Whee42] H.A. Wheeler, "Формулы скин-эффекта",
Труды IRE, vol. 30, нет. 9, стр. 412-424, сентябрь 1942 г.
.. [OwWu58] Г. Х. Оуян и Т. Т. Ву, "Приблизительные параметры слота
Линии и их дополнение" Операции IRE по антеннам и
Распространение, стр. 49-55, январь 1958 г.
.. [Ghio93] G. Ghione, "Аналитическая модель потерь
Общие асимметричные копланарные линии в гибридных и монолитных МИС»
IEEE транс. по теории и технике микроволнового излучения,
об. 41, нет. 9, стр. 1499-1510, сентябрь 1993 г.
"""
Мартинссон, А. Деленив, Э. Коллберг и
И. Вендик, "Простое и точное дисперсионное выражение для
эффективная диэлектрическая проницаемость копланарных волноводов» в
Труды микроволн, антенн и распространения,
об. 144, нет. 2. IEE, 19 апреля.97, стр. 145-148.
.. [Whee42] H.A. Wheeler, "Формулы скин-эффекта",
Труды IRE, vol. 30, нет. 9, стр. 412-424, сентябрь 1942 г.
.. [OwWu58] Г. Х. Оуян и Т. Т. Ву, "Приблизительные параметры слота
Линии и их дополнение" Операции IRE по антеннам и
Распространение, стр. 49-55, январь 1958 г.
.. [Ghio93] G. Ghione, "Аналитическая модель потерь
Общие асимметричные копланарные линии в гибридных и монолитных МИС»
IEEE транс. по теории и технике микроволнового излучения,
об. 41, нет. 9, стр. 1499-1510, сентябрь 1993 г.
""" 68e-8, tand: NumberLike = 0,
f_low: NumberLike = 1e3, f_high: NumberLike = 1e12,
f_epr_tand: NumberLike = 1e9,
has_metal_backside: логическое значение = ложь,
compatibility_mode: Union[str, None] = None,
*args, **kwargs):
Media.__init__(я, частота=частота,z0=z0)
self.w, self.s, self.h, self.t, self.ep_r, self.tand, self.rho =\
w, s, h, t, ep_r, tand, rho
селф.диэль = дил
self.f_low, self.f_high, self.f_epr_tand = f_low, f_high, f_epr_tand
self.has_metal_backside = has_metal_backside
self.compatibility_mode = режим_совместимости
# изменение эффективной диэлектрической проницаемости в зависимости от частоты
# Не реализовано в QUCS, но реализовано в ADS.
# 'частотный инвариант' даст постоянное комплексное значение с реальным
# часть, совместимая с qucs, и мнимая часть из-за tand
self.ep_r_f, self.
68e-8, tand: NumberLike = 0,
f_low: NumberLike = 1e3, f_high: NumberLike = 1e12,
f_epr_tand: NumberLike = 1e9,
has_metal_backside: логическое значение = ложь,
compatibility_mode: Union[str, None] = None,
*args, **kwargs):
Media.__init__(я, частота=частота,z0=z0)
self.w, self.s, self.h, self.t, self.ep_r, self.tand, self.rho =\
w, s, h, t, ep_r, tand, rho
селф.диэль = дил
self.f_low, self.f_high, self.f_epr_tand = f_low, f_high, f_epr_tand
self.has_metal_backside = has_metal_backside
self.compatibility_mode = режим_совместимости
# изменение эффективной диэлектрической проницаемости в зависимости от частоты
# Не реализовано в QUCS, но реализовано в ADS.
# 'частотный инвариант' даст постоянное комплексное значение с реальным
# часть, совместимая с qucs, и мнимая часть из-за tand
self.ep_r_f, self. tand_f = self.analyse_dielectric(
self.ep_r, self.tand,
self.f_low, self.f_high, self.f_epr_tand, self.frequency.f,
селф.диэль)
# квазистатическая эффективная диэлектрическая проницаемость подложки + линии и
# полное сопротивление копланарного волновода
# qucs использует ep_r с действительным знаком, что дает импеданс с действительным знаком
если compatibility_mode == 'qucs':
self.zl_eff, self.ep_reff, k1, kk1, kpk1 = \
self.analyse_quasi_static(
реальный (self.ep_r_f), w, s, h, t, has_metal_backside)
еще:
self.zl_eff, self.ep_reff, k1, kk1, kpk1 = \
self.analyse_quasi_static(
self.ep_r_f, w, s, h, t, has_metal_backside)
# анализировать дисперсию импеданса и относительной диэлектрической проницаемости
если compatibility_mode == 'qucs':
self._z_characteristic, self.ep_reff_f = self.
tand_f = self.analyse_dielectric(
self.ep_r, self.tand,
self.f_low, self.f_high, self.f_epr_tand, self.frequency.f,
селф.диэль)
# квазистатическая эффективная диэлектрическая проницаемость подложки + линии и
# полное сопротивление копланарного волновода
# qucs использует ep_r с действительным знаком, что дает импеданс с действительным знаком
если compatibility_mode == 'qucs':
self.zl_eff, self.ep_reff, k1, kk1, kpk1 = \
self.analyse_quasi_static(
реальный (self.ep_r_f), w, s, h, t, has_metal_backside)
еще:
self.zl_eff, self.ep_reff, k1, kk1, kpk1 = \
self.analyse_quasi_static(
self.ep_r_f, w, s, h, t, has_metal_backside)
# анализировать дисперсию импеданса и относительной диэлектрической проницаемости
если compatibility_mode == 'qucs':
self._z_characteristic, self.ep_reff_f = self. analyse_дисперсия(
self.zl_eff, self.ep_reff, реальный (self.ep_r_f), w, s, h,
собственная.частота.f)
# в объявлениях не используется частотная дисперсия для cpw/cpwg (так грустно)
elif compatibility_mode == 'объявления':
self._z_characteristic = self.zl_eff
self.ep_reff_f = self.ep_reff
# по умолчанию использовать частотную дисперсию и комплексную диэлектрическую проницаемость
еще:
self._z_characteristic, self.ep_reff_f = self.analyse_дисперсия(
self.zl_eff, self.ep_reff, self.ep_r_f, w, s, h,
собственная.частота.f)
# анализируем потери линии
self.alpha_conductor, self.alpha_dielectric = self.analyse_loss(
реальный(self.ep_r_f), реальный(self.ep_reff_f), self.tand_f, ро, 1.,
собственная частота f,
ш, т, с, лиц1, лиц1, лиц1)
analyse_дисперсия(
self.zl_eff, self.ep_reff, реальный (self.ep_r_f), w, s, h,
собственная.частота.f)
# в объявлениях не используется частотная дисперсия для cpw/cpwg (так грустно)
elif compatibility_mode == 'объявления':
self._z_characteristic = self.zl_eff
self.ep_reff_f = self.ep_reff
# по умолчанию использовать частотную дисперсию и комплексную диэлектрическую проницаемость
еще:
self._z_characteristic, self.ep_reff_f = self.analyse_дисперсия(
self.zl_eff, self.ep_reff, self.ep_r_f, w, s, h,
собственная.частота.f)
# анализируем потери линии
self.alpha_conductor, self.alpha_dielectric = self.analyse_loss(
реальный(self.ep_r_f), реальный(self.ep_reff_f), self.tand_f, ро, 1.,
собственная частота f,
ш, т, с, лиц1, лиц1, лиц1) %i-%i %s. %i очков'%\
(f.f_scaled[0],f.f_scaled[-1],f.unit, f.npoints) + \
'\n W= %.2em, S= %.2em'% \
(я.ж, я.ы)
возвратный вывод
def __repr__(self) -> ул:
вернуть себя.__str__()
@имущество
def Z0(self) -> NumberLike:
"""
Волновое сопротивление
"""
вернуть self._z_characteristic
@имущество
def gamma(self) -> NumberLike:
"""
Постоянная распространения.
Возвращает
-------
гамма: :класс:`numpy.ndarray`
"""
ep_reff, f = реальный (self.ep_reff_f), self.frequency.f
альфа = self.alpha_dielectric.copy()
если self.rho не None:
альфа += self.alpha_conductor
бета = 2. * pi * f * sqrt (ep_reff) / c
вернуть альфа + 1j * бета
%i-%i %s. %i очков'%\
(f.f_scaled[0],f.f_scaled[-1],f.unit, f.npoints) + \
'\n W= %.2em, S= %.2em'% \
(я.ж, я.ы)
возвратный вывод
def __repr__(self) -> ул:
вернуть себя.__str__()
@имущество
def Z0(self) -> NumberLike:
"""
Волновое сопротивление
"""
вернуть self._z_characteristic
@имущество
def gamma(self) -> NumberLike:
"""
Постоянная распространения.
Возвращает
-------
гамма: :класс:`numpy.ndarray`
"""
ep_reff, f = реальный (self.ep_reff_f), self.frequency.f
альфа = self.alpha_dielectric.copy()
если self.rho не None:
альфа += self.alpha_conductor
бета = 2. * pi * f * sqrt (ep_reff) / c
вернуть альфа + 1j * бета коэффициента диэлектрических и тангенциальных потерь.
использованная литература
----------
.. [#] К. Свенссон, Г.Е. Дермер,
Моделирование межсоединений с потерями во временной области,
IEEE транс. по усовершенствованной упаковке, май 2001 г., N2, Vol. 24, стр. 191-196.
.. [#] Джорджевич, Р.М. Билич, В.Д. Ликар-Смилянич, Т.К. Саркар,
Широкополосная характеристика FR-4 в частотной области и во временной области
причинность,
IEEE транс. по ЭМС, вып. 43, №4, 2001, с. 662-667.
Возвращает
-------
ep_r_f::class:`numpy.ndarray`
tand_f::class:`numpy.ndarray`
"""
if diel == 'djordjevicsvensson':
# вычислить наклон для логарифмической шкалы частот, зависящий от tanD.
k = log((f_high + 1j * f_epr_tand) / (f_low + 1j * f_epr_tand))
fd = log((f_high + 1j * f) / (f_low + 1j * f))
ep_d = -tand * ep_r / imag(k)
# значение для частоты выше f_high
ep_inf = ep_r * (1.
коэффициента диэлектрических и тангенциальных потерь.
использованная литература
----------
.. [#] К. Свенссон, Г.Е. Дермер,
Моделирование межсоединений с потерями во временной области,
IEEE транс. по усовершенствованной упаковке, май 2001 г., N2, Vol. 24, стр. 191-196.
.. [#] Джорджевич, Р.М. Билич, В.Д. Ликар-Смилянич, Т.К. Саркар,
Широкополосная характеристика FR-4 в частотной области и во временной области
причинность,
IEEE транс. по ЭМС, вып. 43, №4, 2001, с. 662-667.
Возвращает
-------
ep_r_f::class:`numpy.ndarray`
tand_f::class:`numpy.ndarray`
"""
if diel == 'djordjevicsvensson':
# вычислить наклон для логарифмической шкалы частот, зависящий от tanD.
k = log((f_high + 1j * f_epr_tand) / (f_low + 1j * f_epr_tand))
fd = log((f_high + 1j * f) / (f_low + 1j * f))
ep_d = -tand * ep_r / imag(k)
# значение для частоты выше f_high
ep_inf = ep_r * (1. + tand * real(k) / imag(k))
# вычислить комплексную диэлектрическую проницаемость
ep_r_f = ep_inf + ep_d * fd
# встать
tand_f = -imag(ep_r_f) / реальный(ep_r_f)
elif diel == 'частотный инвариант':
ep_r_f = ep_r - 1j * ep_r * tand
tand_f = tand
еще:
поднять ValueError('Неизвестная модель диэлектрической дисперсии')
вернуть ep_r_f, tand_f
+ tand * real(k) / imag(k))
# вычислить комплексную диэлектрическую проницаемость
ep_r_f = ep_inf + ep_d * fd
# встать
tand_f = -imag(ep_r_f) / реальный(ep_r_f)
elif diel == 'частотный инвариант':
ep_r_f = ep_r - 1j * ep_r * tand
tand_f = tand
еще:
поднять ValueError('Неизвестная модель диэлектрической дисперсии')
вернуть ep_r_f, tand_f Модель из [#]_ с воздушной спинкой и [#]_ с металлической спинкой.
Модели скорректированы с учетом
толщины полосы с использованием подхода первого порядка, описанного в [GGBB96]_.
Отчет симулятора ADS для использования пользовательской коррекции на основе [Cohn60]_.
Этот второй метод не реализован в skrf.
использованная литература
----------
.. [GhNa84] Г. Гионе и К. Налди. "Аналитические формулы для копланарных прямых
в гибридных и монолитных МИС», Electronics Letters,
Том. 20, № 4, 16 февраля 1984 г., стр. 179-181.
.. [GhNa83] Г. Гионе и К. Налди. "Параметры копланарных волноводов с
Нижние общие плоскости», Electronics Letters,
Том. 19, № 18, 1 сентября 1983 г., стр. 734-735.
.. [Cohn60] SB Cohn, "Поправки на толщину для емкостных препятствий и
Ленточные проводники», IRE Trans. on Microwave Theory and Techniques,
Том. МТТ-8, ноябрь 1960 г.
Модель из [#]_ с воздушной спинкой и [#]_ с металлической спинкой.
Модели скорректированы с учетом
толщины полосы с использованием подхода первого порядка, описанного в [GGBB96]_.
Отчет симулятора ADS для использования пользовательской коррекции на основе [Cohn60]_.
Этот второй метод не реализован в skrf.
использованная литература
----------
.. [GhNa84] Г. Гионе и К. Налди. "Аналитические формулы для копланарных прямых
в гибридных и монолитных МИС», Electronics Letters,
Том. 20, № 4, 16 февраля 1984 г., стр. 179-181.
.. [GhNa83] Г. Гионе и К. Налди. "Параметры копланарных волноводов с
Нижние общие плоскости», Electronics Letters,
Том. 19, № 18, 1 сентября 1983 г., стр. 734-735.
.. [Cohn60] SB Cohn, "Поправки на толщину для емкостных препятствий и
Ленточные проводники», IRE Trans. on Microwave Theory and Techniques,
Том. МТТ-8, ноябрь 1960 г. , стр. 638-644.
.. [GGBB96] KC Gupta, R. Garg, IJ Bahl, and P. Bhartia, Microstrip
Линии и игровые линии, 2-е изд. Artech House, Inc., 1996.
Возвращает
-------
zl_eff::class:`numpy.ndarray`
ep_reff::class:`numpy.ndarray`
"""
Z0 = кврт (mu_0 / эпсилон_0)
а = ш
б = ш + 2. * с
# уравнение (3a) из [GhNa84] или (6) из [GhNa83]
к1 = а/б
kk1 = эллипсk(k1)
kpk1 = эллипсk(sqrt(1. - k1 * k1))
q1 = эллипа (k1)
# тыльная сторона металлическая
если has_metal_backside:
# уравнение (4) из [GhNa83]
# в qucs коэффициент 2 превращается в 4 и лучше подходит для рекламы
k3 = тангенс (пи * а / 4. / ч) / тангенс (пи * b / 4. / ч)
q3 = эллипа (k3)
qz = 1. / (q1 + q3)
# уравнение (7) из [GhNa83]
# эквивалентно e = (q1 + ep_r * q3) / (q1 + q3) и бумаге
е = 1.
, стр. 638-644.
.. [GGBB96] KC Gupta, R. Garg, IJ Bahl, and P. Bhartia, Microstrip
Линии и игровые линии, 2-е изд. Artech House, Inc., 1996.
Возвращает
-------
zl_eff::class:`numpy.ndarray`
ep_reff::class:`numpy.ndarray`
"""
Z0 = кврт (mu_0 / эпсилон_0)
а = ш
б = ш + 2. * с
# уравнение (3a) из [GhNa84] или (6) из [GhNa83]
к1 = а/б
kk1 = эллипсk(k1)
kpk1 = эллипсk(sqrt(1. - k1 * k1))
q1 = эллипа (k1)
# тыльная сторона металлическая
если has_metal_backside:
# уравнение (4) из [GhNa83]
# в qucs коэффициент 2 превращается в 4 и лучше подходит для рекламы
k3 = тангенс (пи * а / 4. / ч) / тангенс (пи * b / 4. / ч)
q3 = эллипа (k3)
qz = 1. / (q1 + q3)
# уравнение (7) из [GhNa83]
# эквивалентно e = (q1 + ep_r * q3) / (q1 + q3) и бумаге
е = 1. + q3 * qz * (ep_r - 1.)
# уравнение (8) из [GhNa83] с последующим делением на sqrt(e)
zr = Z0 / 2. * qz
# зад воздух
еще:
# уравнение (3b) из [GhNa84]
k2 = sh((pi/4.) * a/h) / sh((pi/4.) * b/h)
q2 = эллипа (k2)
# уравнение (2) из [GhNa84]
е = 1. + (ep_r - 1.) / 2. * q2 / q1
# уравнение (1) из [GhNa84] с последующим делением на sqrt(e)
zr = Z0 / 4. / q1
# апостериорный эффект толщины полосы
если t не None и t > 0.:
# уравнение (7.98) из [GGBB96]
d = 1,25 * t / pi * (1, + log (4, * pi * w / t))
# уравнение между (7.99) и (7.100) из [GGBB96]
# ок. равно ke = (w + d) / (w + d + 2 * (s - d))
кэ = к1 + (1. - к1 * к1) * д / 2. / с
qe = эллипа (ке)
# тыльная сторона металлическая
если has_metal_backside:
# уравнение (8) из [GhNa83] с k1 -> ke
# но оставить q3 без изменений ? (нет в газетах)
qz = 1.
+ q3 * qz * (ep_r - 1.)
# уравнение (8) из [GhNa83] с последующим делением на sqrt(e)
zr = Z0 / 2. * qz
# зад воздух
еще:
# уравнение (3b) из [GhNa84]
k2 = sh((pi/4.) * a/h) / sh((pi/4.) * b/h)
q2 = эллипа (k2)
# уравнение (2) из [GhNa84]
е = 1. + (ep_r - 1.) / 2. * q2 / q1
# уравнение (1) из [GhNa84] с последующим делением на sqrt(e)
zr = Z0 / 4. / q1
# апостериорный эффект толщины полосы
если t не None и t > 0.:
# уравнение (7.98) из [GGBB96]
d = 1,25 * t / pi * (1, + log (4, * pi * w / t))
# уравнение между (7.99) и (7.100) из [GGBB96]
# ок. равно ke = (w + d) / (w + d + 2 * (s - d))
кэ = к1 + (1. - к1 * к1) * д / 2. / с
qe = эллипа (ке)
# тыльная сторона металлическая
если has_metal_backside:
# уравнение (8) из [GhNa83] с k1 -> ke
# но оставить q3 без изменений ? (нет в газетах)
qz = 1. / (qe + q3)
zr = Z0 / 2. * qz
# зад воздух
еще:
# уравнение (7.99) из [GGBB96] с последующим делением на sqrt(e)
zr = Z0 / 4. / qe
# изменяет ep_re
# уравнение (7.100) из [GGBB96]
e = e - (0,7 * (e - 1.) * t/s) / (q1 + (0,7 * t/s))
ep_reff = е
# окончательное деление (1) от [GhNa84] и (8) от [GhNa83]
zl_eff = zr / sqrt (ep_reff)
return zl_eff, ep_reff, k1, kk1, kpk1
/ (qe + q3)
zr = Z0 / 2. * qz
# зад воздух
еще:
# уравнение (7.99) из [GGBB96] с последующим делением на sqrt(e)
zr = Z0 / 4. / qe
# изменяет ep_re
# уравнение (7.100) из [GGBB96]
e = e - (0,7 * (e - 1.) * t/s) / (q1 + (0,7 * t/s))
ep_reff = е
# окончательное деление (1) от [GhNa84] и (8) от [GhNa83]
zl_eff = zr / sqrt (ep_reff)
return zl_eff, ep_reff, k1, kk1, kpk1 . [#] М. Ю. Франкель, С. Гупта, Дж. А. Вальдманис и Г. А. Муру,
"Терагерцовые характеристики затухания и дисперсии компланарных
Линии передачи» IEEE Trans. on Microwave Theory and Techniques,
об. 39, нет. 6, стр. 910-916, июнь 1991 г.
.. [#] С. Геворгян, Т. Мартинссон, А. Деленив, Э. Коллберг и
И. Вендик, "Простое и точное дисперсионное выражение для
эффективная диэлектрическая проницаемость копланарных волноводов» в
Труды микроволн, антенн и распространения,
об. 144, нет. 2. IEE, апрель 1997 г., стр. 145-148.
Возвращает
-------
z::class:`numpy.ndarray`
e::class:`numpy.ndarray`
"""
# частота среза режима TE0
fte = ((c / 4.) / (h * sqrt (ep_r - 1.)))
# коэффициент рассеивания G
р = журнал (Вт / ч)
и = 0,54 - (0,64 - 0,015 * р) * р
v = 0,43 - (0,86 - 0,54 * р) * р
G = exp(u * log(w/s) + v)
# добавляем дисперсионные эффекты в ep_reff
sqrt_ep_reff = sqrt(ep_reff)
sqrt_e = sqrt_ep_reff + (sqrt(ep_r) - sqrt_ep_reff) / \
(1.
. [#] М. Ю. Франкель, С. Гупта, Дж. А. Вальдманис и Г. А. Муру,
"Терагерцовые характеристики затухания и дисперсии компланарных
Линии передачи» IEEE Trans. on Microwave Theory and Techniques,
об. 39, нет. 6, стр. 910-916, июнь 1991 г.
.. [#] С. Геворгян, Т. Мартинссон, А. Деленив, Э. Коллберг и
И. Вендик, "Простое и точное дисперсионное выражение для
эффективная диэлектрическая проницаемость копланарных волноводов» в
Труды микроволн, антенн и распространения,
об. 144, нет. 2. IEE, апрель 1997 г., стр. 145-148.
Возвращает
-------
z::class:`numpy.ndarray`
e::class:`numpy.ndarray`
"""
# частота среза режима TE0
fte = ((c / 4.) / (h * sqrt (ep_r - 1.)))
# коэффициент рассеивания G
р = журнал (Вт / ч)
и = 0,54 - (0,64 - 0,015 * р) * р
v = 0,43 - (0,86 - 0,54 * р) * р
G = exp(u * log(w/s) + v)
# добавляем дисперсионные эффекты в ep_reff
sqrt_ep_reff = sqrt(ep_reff)
sqrt_e = sqrt_ep_reff + (sqrt(ep_r) - sqrt_ep_reff) / \
(1. + G * (f/fte)**(-1,8))
е = sqrt_e**2
z = zl_eff * sqrt_ep_reff / sqrt_e
вернуть г, е
+ G * (f/fte)**(-1,8))
е = sqrt_e**2
z = zl_eff * sqrt_ep_reff / sqrt_e
вернуть г, е .. [#] G. Ghione, "Аналитическая модель, ориентированная на CAD, для потерь
Общие асимметричные копланарные линии в гибридных и монолитных МИС»
IEEE транс. по теории и технике микроволнового излучения,
об. 41, нет. 9, стр. 1499-1510, сентябрь 1993 г.
Возвращает
-------
a_conductor::class:`numpy.ndarray`
a_dielectric::class:`numpy.ndarray`
"""
Z0 = кврт (mu_0 / эпсилон_0)
если t не None и t > 0.:
если ро равно None:
поднять(AttributeError('для расчета необходимо предоставить значения проводимости и толщины проводника. см. справку по инициализатору'))
r_s = поверхностное_сопротивление (f = f, rho = rho, \
мю_р=1)
ds = skin_depth (f = f, rho = rho, mu_r = 1.)
если есть (t < 3 * ds):
предупреждения.предупреждать(
«Расчет потерь в проводнике недействителен для линии»
'высота t ({}) < 3 * глубина кожи ({})'.
.. [#] G. Ghione, "Аналитическая модель, ориентированная на CAD, для потерь
Общие асимметричные копланарные линии в гибридных и монолитных МИС»
IEEE транс. по теории и технике микроволнового излучения,
об. 41, нет. 9, стр. 1499-1510, сентябрь 1993 г.
Возвращает
-------
a_conductor::class:`numpy.ndarray`
a_dielectric::class:`numpy.ndarray`
"""
Z0 = кврт (mu_0 / эпсилон_0)
если t не None и t > 0.:
если ро равно None:
поднять(AttributeError('для расчета необходимо предоставить значения проводимости и толщины проводника. см. справку по инициализатору'))
r_s = поверхностное_сопротивление (f = f, rho = rho, \
мю_р=1)
ds = skin_depth (f = f, rho = rho, mu_r = 1.)
если есть (t < 3 * ds):
предупреждения.предупреждать(
«Расчет потерь в проводнике недействителен для линии»
'высота t ({}) < 3 * глубина кожи ({})'. format(t, ds[0]),
Предупреждение во время выполнения
)
n = (1. - k1) * 8. * pi / (t * (1. + k1))
а = ш/2.
б = а + с
ас = (пи + журнал (п * а)) / а + (пи + журнал (п * б)) / б
a_conductor = r_s * sqrt(ep_reff) * ac / (4. * Z0 * kk1 * kpk1 * \
(1. - лиц.1 * лиц.1))
еще:
a_conductor = нули (f.shape)
l0 = с/f
a_dielectric = pi * ep_r / (ep_r - 1) * (ep_reff - 1) / \
sqrt(ep_reff) * tand / l0
вернуть a_conductor, a_dielectric
format(t, ds[0]),
Предупреждение во время выполнения
)
n = (1. - k1) * 8. * pi / (t * (1. + k1))
а = ш/2.
б = а + с
ас = (пи + журнал (п * а)) / а + (пи + журнал (п * б)) / б
a_conductor = r_s * sqrt(ep_reff) * ac / (4. * Z0 * kk1 * kpk1 * \
(1. - лиц.1 * лиц.1))
еще:
a_conductor = нули (f.shape)
l0 = с/f
a_dielectric = pi * ep_r / (ep_r - 1) * (ep_reff - 1) / \
sqrt(ep_reff) * tand / l0
вернуть a_conductor, a_dielectric