Как узнать координаты земельного участка по кадастровому номеру || KadastrMap.com
Границы земельного надела имеют условную идентификацию, в виде координатных точек. Однако большинство собственников, имея правоустанавливающие документы, например договор купли-продажи, сталкиваются с тем, что есть только кадастровый план, то есть схематическое изображение участка, но нет координатных точек.
Отсутствие координат земельного участка создает препятствия для решения споров с соседями, передачи наследства, а также в ряде случаев затрудняет процесс продажи земельного участка.
Для каких целей необходимо иметь координаты участка
Чтобы определиться, как узнать координаты земельного участка по кадастровому номеру, необходимо внести уточнение информации. Данные по координатным точкам, являются следствием прохождения межевания. Процедуру межевания проводит кадастровый инженер. Если такая процедура пройдена, то можно заказать у нас справки по недвижимости, указав искомый кадастровый номер или по адресу, справки содержат координаты объектов и можно увидеть схематическое расположение участка с координатами. Кадастровый план имеет расшифровку по границам участка, где указываются точные координатные данные. Для дачников и садоводов рекомендуем ознакомиться, что такое технический план СНТ, где имеет ряд особенностей идентификации строений и участков товарищества.
Наличие координатных точек на карте земельного участка имеет гражданско-правовые факторы для различного рода сделок. Чаще всего координаты земельного участка необходимо для нижеуказанных целей.
Если такая процедура пройдена, то можно заказать у нас справки по недвижимости, указав искомый кадастровый номер или по адресу, справки содержат координаты объектов и можно увидеть схематическое расположение участка с координатами. Кадастровый план имеет расшифровку по границам участка, где указываются точные координатные данные. Для дачников и садоводов рекомендуем ознакомиться, что такое технический план СНТ, где имеет ряд особенностей идентификации строений и участков товарищества.
Наличие координатных точек на карте земельного участка имеет гражданско-правовые факторы для различного рода сделок. Чаще всего координаты земельного участка необходимо для нижеуказанных целей.
- Разделение большого земельного надела на несколько мелких. Также, если предусмотрено объединение мелких участков в единое целое.
- Для постановки земельного надела на государственный кадастровый учет.
- Для выделения доли каждого собственника участка, например, при вступлении в наследство.

- Для разрешения споров по земельным вопросам с соседями и иными заинтересованными лицами.
- Для сбора информации, при подготовке земельного надела к продаже или иным действиям, например оформление залога в банке.
- Для обнаружения, с последующим исправлением имеющейся кадастровой ошибки.
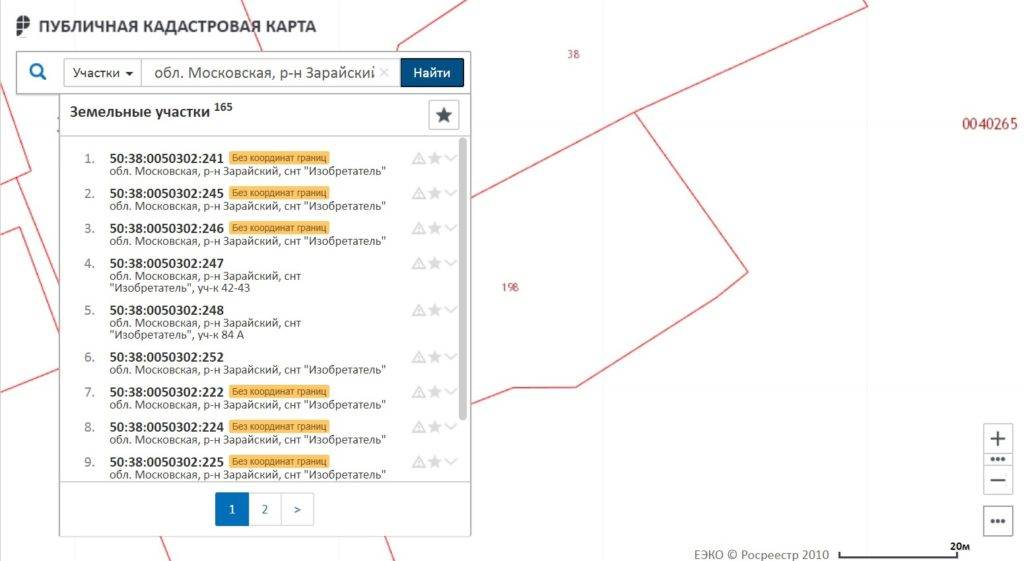
В большинстве случаев, границами земельного надела являются линии соприкосновения с соседними участками. Также линиями соприкосновения являются территории, находящиеся в ведении местных, федеральных властей. В большинстве случаев, визуально границы земельного надела можно увидеть на Публичной кадастровой карте. Это открытый интерактивный сервис кадастровой палаты, в котором собрана вся актуальная информация по земельным участкам.
Как правильно искать информацию о границах земельного участка
Чтобы получить исчерпывающие документальные сведения по земельному наделу, необходимо знать ряд данных, без которого невозможно получить точную информацию о границах участка. Поиск по кадастровому номеру предусматривает введение цифрового идентификатора в виде 01:01:1111111:1. У каждого земельного участка есть собственный уникальный кадастровый шифр земельного надела.
Кадастровый идентификатор означает следующие сведения:
Поиск по кадастровому номеру предусматривает введение цифрового идентификатора в виде 01:01:1111111:1. У каждого земельного участка есть собственный уникальный кадастровый шифр земельного надела.
Кадастровый идентификатор означает следующие сведения:
- 01- кадастровый номер региона, уникальный код региона, например 35- Вологодская область, 77- Москва и т.д.;
- 01- район внутри кадастрового региона, этот номер имеет совпадение с внутритерриториальным делением городов, районов и т.д.;
- 1111111- кадастровый номер земельного квартала, в каждом районе есть территориальное деление по кварталам, которое имеет совпадение по границам населенных пунктов или иных критериев;
- 1 – непосредственный номер земельного участка.
Последние цифры кадастровых идентификаторов имеют 1-2 значения, реже 3 цифры.
Можно ли проверить координатные точки по публичной кадастровой карте
К большому сожалению, публичная кадастровая карта имеет погрешности, поэтому невозможно со 100% гарантией получить точные координатные данные земельного участка. Введя кадастровый номер, вы получите визуальное изображение в виде красных линий. Только заказав выписку из ЕГРН можно получить достоверные данные по координатным точкам. В выписке ЕГРН есть специальный раздел 3, в котором указываются сведения о проведении межевания, с данными по координатам.
Если межевания не было, то в этом разделе будет указана простая схема участка, без расшифровки по координатным точкам. Наличие координатных данных земельного участка закрепляет правовой статус участка с четко обозначенными границами земли. Эти сведения можно использовать при различных спорах с соседями, предоставлять заинтересованным лицам и т.д. Если вы не знаете точный кадастровый идентификатор земельного надела, поиск можно осуществлять, указав известный физический адрес месторасположения участка.
Введя кадастровый номер, вы получите визуальное изображение в виде красных линий. Только заказав выписку из ЕГРН можно получить достоверные данные по координатным точкам. В выписке ЕГРН есть специальный раздел 3, в котором указываются сведения о проведении межевания, с данными по координатам.
Если межевания не было, то в этом разделе будет указана простая схема участка, без расшифровки по координатным точкам. Наличие координатных данных земельного участка закрепляет правовой статус участка с четко обозначенными границами земли. Эти сведения можно использовать при различных спорах с соседями, предоставлять заинтересованным лицам и т.д. Если вы не знаете точный кадастровый идентификатор земельного надела, поиск можно осуществлять, указав известный физический адрес месторасположения участка.
Получить полную информацию о вашем объекте недвижимости
Получить информацию об вашем объекте
Как определить границы земельного участка самостоятельно
Определение границ земельного участка на местности, в первую очередь, необходимо для его собственника. Это связано с тем, что владение землей – это не только права на объект недвижимости, но еще и обязанность уплачивать с него налоги. Так как обязательным межевание земельного участка стало только с 1 января 2018 года, для многих наделов границы по-прежнему не установлены. Как узнать, как правильно определить границы земельного участка и зачем это нужно, читайте ниже.
Это связано с тем, что владение землей – это не только права на объект недвижимости, но еще и обязанность уплачивать с него налоги. Так как обязательным межевание земельного участка стало только с 1 января 2018 года, для многих наделов границы по-прежнему не установлены. Как узнать, как правильно определить границы земельного участка и зачем это нужно, читайте ниже.
Содержание:
- Определение границ земельного участка
- Юридические и фактические границы земельного участка
- Как определить границы земельного участка?
- Что делать в случае спора с соседями?
- Что делать, когда для спора нет оснований?
Определение границ и размера земельного участка
Определение границ земельного участка — это процедура, в которой происходит определение поворотных точек участка с привязкой к GPS координатам (границ) и фиксирование их в едином Государственном кадастре недвижимости.
С 1 января 2018 года в отношении всех земельных участков должно проводиться межевание. Данные о границах вносятся в ЕГРН при постановке земельного участка на кадастровый учет. Так сложилось, что раньше межевание не было обязательной процедурой. И в отношении ранее зарегистрированных земельных участков нередко можно встретить запись «границы не установлены».
Юридические и фактические границы земельного участка
Границы и площадь земельного участка – это две важных его характеристики. По сути граница является некой условной линией, соединяющей две поворотные точки.
Представим себе обычный четырехугольный участок. Он имеет 4 поворотные точки в каждом углу. Линия между ними будет границей. Для многоконтурных участков таких точек будет больше.
Во время кадастровых исследований инженер устанавливает местоположение координат характерных точек границ земельных участков, а уже затем соединит их линиями на плане. Эти линии и будут границами. От того, насколько точно установлены координаты поворотных точек, будет зависеть точность определения границ. При постановке земли на кадастровый учет, указываются не длины границ, как это могло бы показаться, а координаты характерных точек. Только таким образом можно однозначно определить местоположение земельного участка, исключив вероятность разночтений.
При постановке земли на кадастровый учет, указываются не длины границ, как это могло бы показаться, а координаты характерных точек. Только таким образом можно однозначно определить местоположение земельного участка, исключив вероятность разночтений.
Для установления границ земельного участка и проводится процедура межевания. Тем не менее, говорить о том, что в отношении вашего земельного участка установлены границы можно только после того, как необходимые данные будут внесены в Кадастр. Узнать, было ли межевание, очень просто. Посмотрите в кадастровой выписке характеристики вашего участка. Если границы устанавливались, все данные будут указаны в этом документе.
Определение точных границ земельного участка, в первую очередь, необходимо владельцу надела, так как оно позволяет защитить права собственника. Несмотря на это, даже при проведенном межевании можно оказаться вовлеченным в граничный спор с соседями. Это имеет несколько причин. Во-первых, во время определения координат поворотных точек существует погрешность, допускаемая законом. Во-вторых, на местности эти точки могут выглядеть по-разному. В результате не редко встречаются ситуации, когда фактическая граница проходит внутри ранее построенного здания. Еще чаще фактические границы проходят вдоль заборов, стен зданий, могут быть представлены колышками.
Во-вторых, на местности эти точки могут выглядеть по-разному. В результате не редко встречаются ситуации, когда фактическая граница проходит внутри ранее построенного здания. Еще чаще фактические границы проходят вдоль заборов, стен зданий, могут быть представлены колышками.
Для того чтобы фактическая граница была установлена в соответствие с законом, она должна соответствовать данным из кадастра. То есть, если ваш забор между двумя участками проходит по линии между поворотными точками, все законно.
Как определить границы земельного участка?
Определение местоположения земельного участка на местности осуществляется несколькими законными способами:
- По факту. Такое установление применяется в том случае, если земельный участок не был размежеван. В этом случае вам потребуется заказать услугу межевания и определить границы земельного участка. Когда с соседями нет споров, определение кадастровых границ проходит быстро. Они устанавливаются по межевым знакам, после чего собственники смежных участков подписывают акт согласования границ.

- По кадастровой информации в Росреестре. Этот способ установления границ применим в тех случаях, когда межевание было проведено, но по факту никаких разграничивающих знаков между участками нет. В этом случае требуется не столько определение координат границ земельных участков, сколько вынос границ в натуру. За основу берется информация, указанная в кадастре. По этим данным устанавливаются межевые знаки.
Теоретически, определение земельных границ участка осуществляется довольно просто, но на практике возникает много сложностей. Чаще всего проблемы возникают на этапе согласования установленных границ объекта землеустройства. Они могут быть вызваны разными причинами:
- Соседи не согласны.
 При установке местоположения границ по факту соседи нередко высказывают несогласие. Особенно часто это встречается в тех случаях, когда еще до установления границ между владельцами смежных участков шел спор из-за земли.
При установке местоположения границ по факту соседи нередко высказывают несогласие. Особенно часто это встречается в тех случаях, когда еще до установления границ между владельцами смежных участков шел спор из-за земли. - Соседей найти невозможно. Соседний участок давно заброшен, и кому он принадлежит вы не знаете. Раньше такая ситуация была почти неразрешимой. Сейчас закон устанавливает регламент, позволяющий реализовать определение границ дачного участка даже в этом случае. Тем не менее, нужно быть готовым к тому, что в сложных случаях это потребует дополнительных временных затрат.
- Во время установления границ обнаружились кадастровые ошибки. Еще одна из частых проблем, возникающих при установлении фактических границ. Кадастровый инженер устанавливает границы, начинает их наложение на кадастровую карту и обнаруживает ошибки. Исправление таких ошибок затрагивает интересы не только владельцев смежных ЗУ, иногда в спор оказывается вовлечено гораздо больше заинтересованных лиц.
 Например, при межевании одного из земельных участков была допущена ошибка, а границы следующих участков установили по отношению к ошибочным данным. В таких случаях сложно дать один универсальный совет. Каждая ситуация – индивидуальна, и решение должно приниматься с учетом конкретных данных.
Например, при межевании одного из земельных участков была допущена ошибка, а границы следующих участков установили по отношению к ошибочным данным. В таких случаях сложно дать один универсальный совет. Каждая ситуация – индивидуальна, и решение должно приниматься с учетом конкретных данных.
Что делать в случае спора с соседями?
Когда вы оказываетесь в ситуации граничного спора с соседями, в первую очередь, постарайтесь договориться. Если определение координат участка на местности спровоцировало разногласия между собственниками смежных владений, нужно находить компромисс. Споры о прохождении границы участка в натуре можно решить разными способами:
- Определение погрешности. Как мы уже говорили, закон устанавливает допустимую погрешность при установлении границ. Величина этой погрешности различается в зависимости от категории земли. Обычно, если спор идет из-за нескольких десятков сантиметров, оказывается, что они находятся в пределах погрешности.
- Вынос в натуру.
 Это кадастровая процедура, позволяющая установить точное местоположение земельного участка на местности. Поэтому будьте готовы нести дополнительные затраты. Кадастровый инженер на основе данных из ГКН устанавливает на местности поворотные точки.
Это кадастровая процедура, позволяющая установить точное местоположение земельного участка на местности. Поэтому будьте готовы нести дополнительные затраты. Кадастровый инженер на основе данных из ГКН устанавливает на местности поворотные точки.
Самым сложным и дорогостоящим вариантом урегулирования спора является землеустроительная экспертиза. Кадастровый инженер анализирует ситуацию и выявляет причину развития спорной ситуации. После этого он составляет свое заключение с рекомендациями по устранению выявленных проблем.
Когда соседи не готовы к мирному диалогу относительно спорных границ смежных земельных участков, единственный вариант – обращение в суд. Такой подход потребует времени, дополнительных затрат, но решение суда окончательно поставит точку в споре. Нужно быть готовым к тому, что вам все равно придется проводить землеустроительную экспертизу, так как в делах по земельным спорам она назначается практически всегда.
Что делать, когда для спора нет оснований?
Случаи, когда соседи десятилетиями спорят буквально из-за нескольких сантиметров, превращая спор в настоящую войну, не редкость.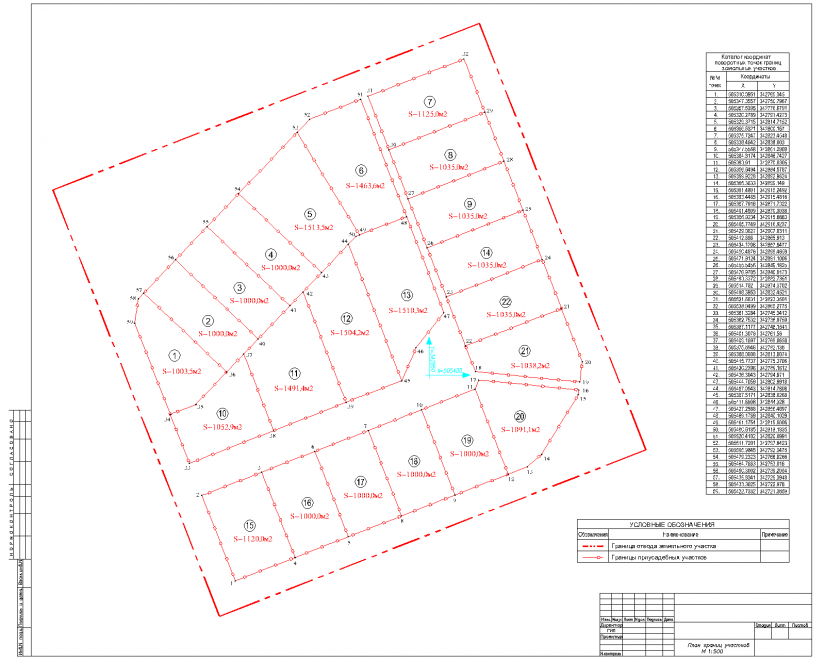 При этом законные основания для такого спора есть далеко не всегда. Дело в том, что определить координаты поворотных точек границ участка с абсолютной точностью без погрешности невозможно.
При этом законные основания для такого спора есть далеко не всегда. Дело в том, что определить координаты поворотных точек границ участка с абсолютной точностью без погрешности невозможно.
Погрешность в замерах есть всегда, а на ее величину могут влиять разные факторы:
- Точность прибора. Для определения координат используют геодезическое оборудование, которое должно регулярно проходить проверки. К сожалению, гарантировать, что оборудование дает минимальную погрешность, могут только крупные специализированные компании. Небольшие компании или частные специалисты не имеют своего оборудования и проводят замеры арендованными приборами. Погрешность в таком случае может сильно выходить за допустимые пределы.
- Метод измерений. В геодезии используют разные методы, и все они дают разную погрешность.
- Квалификация специалиста. Тот факт, что частный специалист имеет лицензию, совершенно не подтверждает его высокую квалификацию. Рекомендуем вам перед заключением договора проверять на сайте Росреестра не только информацию о лицензиях и допусках, но и количество отказов.
 Обращаясь в компанию «Геомер групп», вы можете быть уверены в квалификации и, что тоже немаловажно, опыте кадастрового инженера, который будет заниматься вашим вопросом.
Обращаясь в компанию «Геомер групп», вы можете быть уверены в квалификации и, что тоже немаловажно, опыте кадастрового инженера, который будет заниматься вашим вопросом.
При проведении межевания кадастровый инженер должен не просто определить координаты поворотных точек земельного участка, но и сделать это таким образом, чтобы минимизировать возможную погрешность. Она не должна выходить за установленные допуски. Они определяются Приказом Минэкономразвития №518 и зависят от категории земли. Приведем некоторые допуски:
- Для населенных пунктов – 0,1 м.
- Для дачных участков, земель для садоводства и огородничества, ЛПХ – 0,2 м.
- Земли сельхозназначения – 2,5 метра.
Местоположение фактической границы участка может колебаться в пределах установленной нормы, и это не является нарушением закона. Но и здесь все не так просто, как может показаться. Дело в том, что до 2013 года существовали другие нормы погрешности. Так, например, для садоводческих участков, земель ЛПХ норма устанавливалась в 0,3 метра.
На практике это выглядит примерно следующим образом. Например, у вас есть садоводческий земельный участок, границы которого были установлены до 2013 года. Все исследования были проведены в соответствии с действовавшими тогда нормами, и погрешность не превышает действовавших на тот момент 0,3 метра. Но по новым нормам она должна быть 0,2 метра. К сожалению, в этом случае вам придется уточнять границы участка, так как положение закона утратило свою силу.
Узнать точность, с которой было проведено определение координат поворотных точек вашего участка, можно в кадастровой выписке. Если оно находится в пределах нормы, оснований для граничного спора нет.
Мы советуем в случае малейших сомнений обращаться к специалистам — кадастровым инженерам. Земельное законодательство не просто сложная отрасль. Оно находится в стадии становления, в него регклярно вносятся изменения. Специалист разберет конкретно вашу ситуацию и даст рекомендации, как лучше поступить в данном случае.
Источник: https://geomergroup. ru/article/opredelenie-granic-zemelnogo-uchastka.html
ru/article/opredelenie-granic-zemelnogo-uchastka.html
Координатные графики
Координатная геометрия имеет дело с графическим (или построением) и анализом точек, линий и областей на координатной плоскости (координатный график). Каждой точке на числовой прямой присваивается номер. Точно так же каждой точке на плоскости ставится в соответствие пара чисел. Эти числа представляют размещение точки относительно двух пересекающихся линий. В координатных графиках (см. рис. 1) используются две перпендикулярные числовые линии, которые называются координатными осями. Одна ось является горизонтальной и называется осью x . Другая — вертикальная и называется осью y . Точка пересечения двух числовых линий называется началом координат и представлена координатами (0, 0).
Рис. 1. График координат x-y .
Каждая точка на плоскости расположена уникальной упорядоченной парой чисел, называемой координаты. Некоторые координаты отмечены на Рис. 2.
Некоторые координаты отмечены на Рис. 2.
Рис. 2. Нанесение координат на график.
Обратите внимание, что на оси x числа справа от 0 положительные, а слева от 0 отрицательные. На оси y числа выше 0 являются положительными, а ниже 0 — отрицательными. Также обратите внимание, что первое число в упорядоченной паре называется x – координата, или – абсцисса, , а второе число – 9.0003 y ‐координата, или ордината. Координата x показывает направление вправо или влево, а координата y показывает направление вверх или вниз.
График координат разделен на четыре четверти, называемые квадрантами. Эти квадранты помечены на рисунке 3.
Рисунок 3. График координат с помеченными квадрантами.
Обратите внимание на следующее:
- В квадранте I, x всегда положителен, а y всегда положителен.

- В квадранте II x всегда отрицательно, а y всегда положительно.
- В квадранте III x и y всегда отрицательны.
- В квадранте IV x всегда положительно, а y всегда отрицательно.
Нанесение уравнений на координатную плоскость
К Нанесение уравнения на координатную плоскость , найдите координату, присвоив значение одной переменной и решив полученное уравнение для другого значения. Повторите этот процесс, чтобы найти другие координаты. (При задании значения одной переменной вы можете начать с 0, затем попробовать 1 и т. д.) Затем нарисуйте решения.
Пример 1
Нарисуйте уравнение x + y = 6.
Полезно использовать простую диаграмму.
х
у
| 0 | 6
| 1 | 5
| 2 | 4
Теперь нанесите эти координаты, как показано на рисунке 4.
Рисунок 4. Нанесение координат (0,6), (1,5), (2,4) образуют прямую линию. Уравнения, множества решений которых образуют прямую линию, называются линейными уравнениями. Дополните график x + y = 6, проведя линию, проходящую через эти точки (см. рис. 5).
Уравнения, множества решений которых образуют прямую линию, называются линейными уравнениями. Дополните график x + y = 6, проведя линию, проходящую через эти точки (см. рис. 5).
Рисунок 5. Линия, проходящая через точки, изображенные на рисунке 4.
Уравнения, в которых переменная возводится в степень, показывает деление на переменную, включает переменные с квадратными корнями или имеют переменные, умноженные вместе, не будут образовывать прямую линию при графическом отображении их решений. Они называются нелинейными уравнениями.
Пример 2
Нарисуйте уравнение y = x 2 + 4.
Используйте простую диаграмму.
х
у
| -2 | 8
| -1 | 5
| 0 | 4
| 1 | 5
| 2 | 8
Теперь нанесите эти координаты, как показано на рис. 6.
Обратите внимание, что эти решения при построении не образуют прямую линию.
Эти решения при нанесении на график дают кривую линию (нелинейную). Чем больше точек нанесено, тем проще увидеть и описать набор решений.
Рис. 6. Нанесение координат на простой график.
Завершить график y = x 2 + 4, соединив эти точки плавной кривой, проходящей через эти точки (см. рис. 7).
Рисунок 7. Линия, проходящая через точки, изображенные на рисунке 6.
Наклон и точка пересечения линейных уравнений
Между графиком линейного уравнения и самим уравнением существуют две зависимости, на которые следует обратить внимание. Один включает наклон линии , , а другой касается точки, где 9Линия 0008 пересекает ось Y. Чтобы увидеть любое из этих соотношений, члены уравнения должны стоять в определенном порядке.
(+)(1) y = ( ) x + ( )
Когда термины записаны в таком порядке, говорят, что уравнение имеет форму y . Y ‐форма написана y = m x + b 0008 м и б .
Пример 3
Запишите уравнения в форме y .
- y = -2 x + 1 (уже в форме y )
Как показано на графиках трех задач на рисунке 8, линии пересекают ось y в точках –3, +1 и –2, последнем члене в каждом уравнении.
Если линейное уравнение записывается в виде y = mx + b, b это y ‐перехват.
Наклон линии определяется как
, а слово «изменение» относится к разнице значений y (или x ) между двумя точками на линии.
Примечание: точек A и B могут быть любыми двумя точками на линии; разницы в наклоне не будет.
Рисунок 8. Графики, показывающие линии, пересекающие и -ось.
Пример 4
Найдите наклон x – y = 3, используя координаты.
Чтобы найти наклон линии, выберите любые две точки на линии, например A (3, 0) и B (5, 2), и рассчитайте наклон.
Пример 5
Найдите наклон y = –2 x – 1, используя координаты.
Выберите две точки, например A (1, –3) и B (–1, 1) и рассчитайте наклон.
Пример 6
Найдите наклон x – 2 y = 4, используя координаты.
Выберите две точки, например A (0, –2) и B (4, 0), и рассчитайте наклон.
Возвращаясь к уравнениям для примера (a), (b) и (c), записанным в форме y , должно быть очевидно, что наклон линии равен числовому коэффициенту x ‐ срок.
Построение графика линейных уравнений с использованием наклона и точки пересечения
Построение графика уравнения с использованием его наклона и y‐ точки пересечения обычно довольно просто.
- Запишите уравнение в форме y‐ .
- Найдите точку пересечения и на графике (то есть одну из точек на линии).
- Запишите наклон в виде отношения (доли) и используйте его для поиска других точек на линии.

- Проведите линию через точки.
Пример 7
Нарисуйте уравнение x – y = 2, используя наклон и точку пересечения y‐ .
Найдите –2 на оси y‐ и от этой точки посчитайте, как показано на рисунке 9:
наклон = 1
Рисунок 9. График линии y x 9000. Пример 8
Постройте график уравнения 20009 ‐перехват.
Найдите +4 на оси y и от этой точки отсчитайте, как показано на рисунке 10:
наклон = 2
4.
Пример 9
Нарисуйте уравнение x + 3 y = 0, используя наклон и y — точку пересечения.
Найдите 0 на оси y и отсчитайте от этой точки, как показано на рисунке 11:
Рис. 11. График прямой x + 3 y = 0.
Нахождение уравнения прямой
Нахождение уравнения прямой при работе с упорядоченными парами, наклонами и точками пересечения , используйте один из следующих подходов в зависимости от того, какую форму уравнения вы хотите иметь. Существует несколько форм, но наиболее распространены три формы: форма с пересечением наклона , форма с точкой-наклоном и стандартная форма . Форма пересечения наклона выглядит следующим образом: y = m x + b , где m — это наклон линии, а b — это y – точка пересечения. Форма точка -склопа выглядит как Y — Y 1 = M ( x — x 1 ), где M — это склон и ( x 1 10009 — это склон и ( x 1 10009. , y 1 ) — любая точка на прямой. Стандартная форма выглядит как Ax + By = C , где, если возможно, A , B и C являются целыми числами.
Существует несколько форм, но наиболее распространены три формы: форма с пересечением наклона , форма с точкой-наклоном и стандартная форма . Форма пересечения наклона выглядит следующим образом: y = m x + b , где m — это наклон линии, а b — это y – точка пересечения. Форма точка -склопа выглядит как Y — Y 1 = M ( x — x 1 ), где M — это склон и ( x 1 10009 — это склон и ( x 1 10009. , y 1 ) — любая точка на прямой. Стандартная форма выглядит как Ax + By = C , где, если возможно, A , B и C являются целыми числами.
Форма пересечения наклона.
- Найти уклон, м .
- Найдите точку пересечения y , b .

- Подставьте наклон и y -пересечение в форму наклона-пересечения, y = m x + b .
Точечно-наклонная форма.
- Найти уклон, м .
- Используйте любую точку на линии.
- Подставьте наклон и упорядоченную пару точек в форму точка-наклон, y – y 1 = м ( x – x 1 ).
Примечание: Вы можете начать с формы точка-наклон для уравнения линии, а затем решить уравнение для лет. Вы получите форму пересечения наклона без необходимости сначала находить г – перехват.
Стандартная форма.
- Найдите уравнение линии, используя либо форму наклон-пересечение, либо форму точка-наклон.
- С помощью соответствующей алгебры устройте так, чтобы получить x -членов и y -членов с одной стороны уравнения и константу с другой стороны уравнения.

- Если необходимо, умножьте каждую часть уравнения на наименьший общий знаменатель всех знаменателей, чтобы получить все целые коэффициенты для переменных.
Пример 10
Найдите уравнение линии в форме точки пересечения, когда м = – 4 и b = 3. Затем преобразуйте его в стандартную форму.
- Найти уклон, м .
- м = – 4 (дано)
- Найдите точку пересечения с осью Y, b .
- б = 3 (дано)
- Подставьте наклон и y -пересечение в форму наклон-пересечение, y = м х + б .
- y = – 4 x + 3 (форма пересечения наклона)
- С помощью соответствующей алгебры устройте так, чтобы получить x -членов и y -членов с одной стороны уравнения и константу с другой стороны уравнения.
Пример 11
Найдите уравнение прямой в форме точка-наклон, проходящей через точку (6, 4) с наклоном –3. Затем преобразовать его в стандартный вид.
Затем преобразовать его в стандартный вид.
- Найти уклон, м .
- м = –3 (дано)
- Используйте любую точку на линии.
- (6, 4) (дано)
- Подставьте наклон и упорядоченную пару точек в форму точка-наклон,
- С помощью соответствующей алгебры устройте так, чтобы получить x -членов и y -членов с одной стороны уравнения и константу с другой стороны уравнения.
Пример 12
Найдите уравнение прямой в форме точки-точки пересечения или точки-наклона, проходящей через точки (5, –4) и (3, 7). Затем преобразовать его в стандартный вид.
Пуск с пересечением наклона:
- Найдите точку пересечения y , b .
- Подставьте наклон и любую точку в форму пересечения наклона.
- Замените наклон и y -пересечение в форме наклон-пересечение, y = м х + б.
- С помощью соответствующей алгебры устройте так, чтобы получить x -членов и y -членов с одной стороны уравнения и константу с другой стороны уравнения.

- Если необходимо, умножьте каждую часть уравнения на наименьший общий знаменатель всех знаменателей, чтобы получить все целые коэффициенты для переменных.
Начиная с формы точка-наклон:
- Используйте любую точку на линии.
- (3, 7) (дано)
- Подставьте наклон и упорядоченную пару точек в форму точка-наклон,
- С помощью соответствующей алгебры устройте так, чтобы получить x -членов и y -членов с одной стороны уравнения и константу с другой стороны уравнения.
- Если необходимо, умножьте каждую часть уравнения на наименьший общий знаменатель, чтобы получить все целые коэффициенты для переменных.
Нанесение точек на график или плоскость XY
Поиск В этом уроке я подготовил восемь (8) проработанных примеров того, как нанести точку на декартовой плоскости (названной в честь французского математика Рене Декарта). Чтобы нанести точку, нам нужно две вещи: точка и координатная плоскость .
Кратко расскажем о каждом из них.
A Точка
Точка на плоскости содержит два компонента, порядок которых имеет значение! Он представлен в виде (x,y), где x стоит первым, а y вторым.
- Значение x указывает, как точка перемещается вправо или влево по оси x . Эта ось является основной горизонтальной линией прямоугольной оси или декартовой плоскости.
- Значение y указывает, как точка перемещается вверх или вниз по оси y. Эта ось представляет собой основную вертикальную линию прямоугольной оси или декартовой плоскости.
КООРДИНАТНАЯ ПЛОСКОСТЬ (Декартова плоскость)
Координатная плоскость состоит из две линии, пересекающиеся под углом 90 градусов (что делает их перпендикулярными линиями) в точке (0,0) , известной как начало координат .
- Компонент x точки (x,y) перемещает точку по горизонтальной линии.
 Если значение x положительное, точка перемещается на «x единиц» вправо. С другой стороны, если значение x отрицательно, точка перемещается на «x единиц» влево.
Если значение x положительное, точка перемещается на «x единиц» вправо. С другой стороны, если значение x отрицательно, точка перемещается на «x единиц» влево.
- Компонент Y точки (x,y) перемещает точку по вертикальной линии. Если значение y положительно, точка перемещается на «y-единиц» вверх. Однако, если значение y отрицательно, точка перемещается на «y-единицы» в направлении вниз.
Квадранты декартовой плоскости
Пересечение осей x и y приводит к четырём (4) сечениям или делениям декартовой плоскости.
- Первый квадрант расположен в верхней правой части плоскости.
- Второй квадрант расположен в верхней левой части плоскости.
- Третий квадрант расположен в нижней левой части плоскости.
- Четвертый квадрант расположен в нижней правой части плоскости.
Примеры нанесения точек на график и определения его квадранта
Пример 1 : Нанесите точку (4,2) и определите, в каком квадранте или оси она расположена.
Я начну с размещения точки в начале координат – пересечении осей x и y. Думайте о начале координат как о «доме», откуда берутся все точки.
Затем я сдвину точку из исходной точки на 4 единицы вправо , так как x = 4 (положительное значение по оси x означает движение вправо). Помните, что значение x — это первое число в упорядоченной паре (4,2).
С того места, где я остановился, мне нужно переместиться на две единицы вверх, параллельно основной вертикальной оси, поскольку y = 2 (положительное значение по оси y означает движение вверх). Значение y — это второе число в упорядоченной паре (4,2).
Окончательный ответ должен выглядеть следующим образом…
Точка (4,2) находится в Квадранте I .
Пример 2 : Нанесите точку (–5, 4) и определите, в каком квадранте или оси она находится.
Начните с размещения точки в начале координат, известном как центр декартовой оси координат.
Из исходной точки, так как x = −5 , переместиться на 5 единиц влево .
… с последующим перемещением точки на 4 единицы вверх , потому что y = 4 .
Это окончательный ответ. Поскольку нанесенная точка находится в верхней левой части оси xy, она должна находиться в квадранте II.
Пример 3 : Нанесите точку (5, –3) и определите, в каком квадранте или оси она находится.
Начните с центра декартовой плоскости.
Переместить на 5 единиц вправо , так как x = 5 .
Далее следует перемещение на 3 единицы вниз с y = −3 .
Окончательная точка на графике показана ниже. Нахождение в нижней правой части декартовой плоскости означает, что она находится в квадранте IV.
Пример 4 : Нанесите точку (–2, –5) и определите, в каком квадранте или оси она находится.
Поместите точку в исходную точку (центр оси xy). Поскольку x = −2 , переместите точку на 2 единицы влево на по оси x. Наконец, опускаются на 5 единиц параллельно оси у, потому что у = −5 .
См. анимированное решение ниже.
Нанесенная точка находится в нижней левой части декартовой плоскости. Таким образом, он находится в квадранте III.
Пример 5 : Нанесите точку (0,3) и определите, в каком квадранте или оси она находится.
Я начинаю с анализа данной упорядоченной пары. Поскольку x = 0 , это означает, что нет движения по оси x . Тем не менее, = 3 означает, что мне нужно переместить его на 3 единицы вверх .
Нанесенная точка не равна ни ни в квадранте I, ни в квадранте II. Чтобы описать его местоположение, мы говорим, что оно находится вдоль положительной оси ординат.
Пример 6 : Нанесите точку (0, –4) и определите, в каком квадранте или оси она находится.
Это очень похоже на пример 5. Движения по оси x не будет, так как x = 0 . С другой стороны, y = − 4 говорит мне, что мне нужно переместить точку из начала координат на 4 единицы вниз на .
Конечная точка находится не в ни в квадранте III, ни в квадранте IV. Я могу утверждать, что он находится вдоль отрицательной оси Y.
Пример 7 : Нанесите точку (–3,0) и определите, в каком квадранте или оси она находится.
От исходной точки я сдвину на 3 единицы влево по оси x, поскольку x = −3. Для y = 0 это означает, что никакого движения по оси Y не последует.
Точка расположена ни в ни в квадранте II, ни в квадранте III.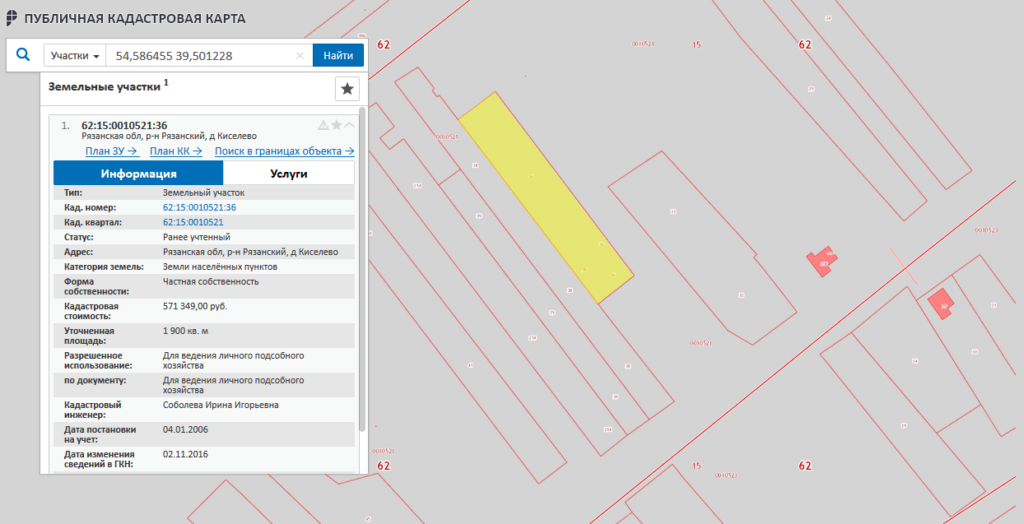



 При установке местоположения границ по факту соседи нередко высказывают несогласие. Особенно часто это встречается в тех случаях, когда еще до установления границ между владельцами смежных участков шел спор из-за земли.
При установке местоположения границ по факту соседи нередко высказывают несогласие. Особенно часто это встречается в тех случаях, когда еще до установления границ между владельцами смежных участков шел спор из-за земли. Например, при межевании одного из земельных участков была допущена ошибка, а границы следующих участков установили по отношению к ошибочным данным. В таких случаях сложно дать один универсальный совет. Каждая ситуация – индивидуальна, и решение должно приниматься с учетом конкретных данных.
Например, при межевании одного из земельных участков была допущена ошибка, а границы следующих участков установили по отношению к ошибочным данным. В таких случаях сложно дать один универсальный совет. Каждая ситуация – индивидуальна, и решение должно приниматься с учетом конкретных данных. Это кадастровая процедура, позволяющая установить точное местоположение земельного участка на местности. Поэтому будьте готовы нести дополнительные затраты. Кадастровый инженер на основе данных из ГКН устанавливает на местности поворотные точки.
Это кадастровая процедура, позволяющая установить точное местоположение земельного участка на местности. Поэтому будьте готовы нести дополнительные затраты. Кадастровый инженер на основе данных из ГКН устанавливает на местности поворотные точки.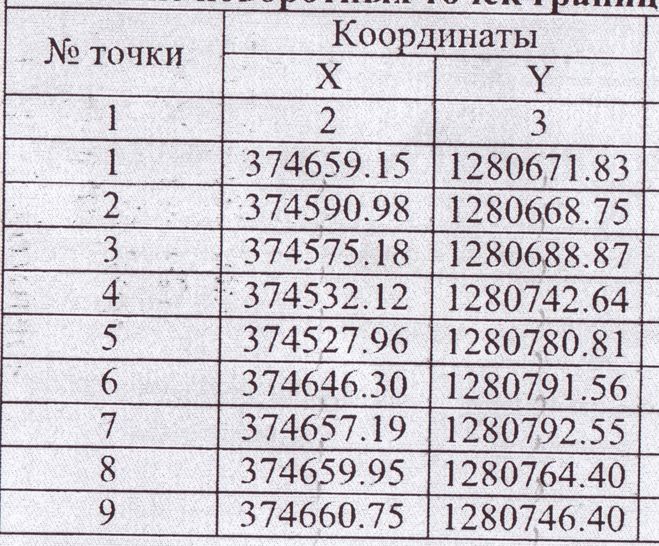 Обращаясь в компанию «Геомер групп», вы можете быть уверены в квалификации и, что тоже немаловажно, опыте кадастрового инженера, который будет заниматься вашим вопросом.
Обращаясь в компанию «Геомер групп», вы можете быть уверены в квалификации и, что тоже немаловажно, опыте кадастрового инженера, который будет заниматься вашим вопросом.


 Если значение x положительное, точка перемещается на «x единиц» вправо. С другой стороны, если значение x отрицательно, точка перемещается на «x единиц» влево.
Если значение x положительное, точка перемещается на «x единиц» вправо. С другой стороны, если значение x отрицательно, точка перемещается на «x единиц» влево.